Question
I have the solution, but can anyone explain to me how to reach the final output? A diagram would be nice. Given the following implementation
I have the solution, but can anyone explain to me how to reach the final output? A diagram would be nice.
Given the following implementation of a gated(clocked) S-R latch
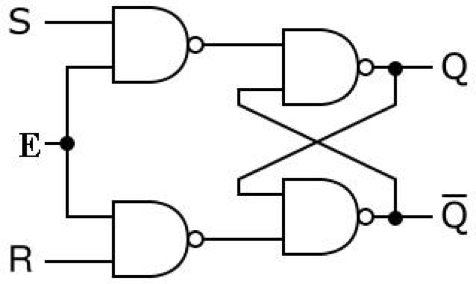
fill in its truth table:
| E | Q(t) | S(t) | R(t) | Q(t+1) |
| 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 1 | 0 |
| 0 | 0 | 1 | 0 | 0 |
| 0 | 0 | 1 | 1 | 0 |
| 0 | 1 | 0 | 0 | 1 |
| 0 | 1 | 0 | 1 | 1 |
| 0 | 1 | 1 | 0 | 1 |
| 0 | 1 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 1 | 0 |
| 1 | 0 | 1 | 0 | 1 |
| 1 | 0 | 1 | 1 | ? |
| 1 | 1 | 0 | 0 | 1 |
| 1 | 1 | 0 | 1 | 0 |
| 1 | 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 | ? |
use ? for undefined states (i.e., when ).
Q(t), S(t), R(t) are the values of Q, S and R at time t, while Q(t+1) is the value of Q at time t+1 (after applying new inputs).
[O SStep by Step Solution
There are 3 Steps involved in it
Step: 1
Get Instant Access to Expert-Tailored Solutions
See step-by-step solutions with expert insights and AI powered tools for academic success
Step: 2
Step: 3
Ace Your Homework with AI
Get the answers you need in no time with our AI-driven, step-by-step assistance
Get Started
Advances In Databases And Information Systems 14th East European Conference Adbis 2010 Novi Sad Serbia September 2010 Proceedings Lncs 6295
Authors: Barbara Catania ,Mirjana Ivanovic ,Bernhard Thalheim
2010th Edition
3642155758, 978-3642155758
