I just need the questuin (2.10) answered. I have provided the solution for the example but i need the new data for 2.10. Please show work/plot thanks!

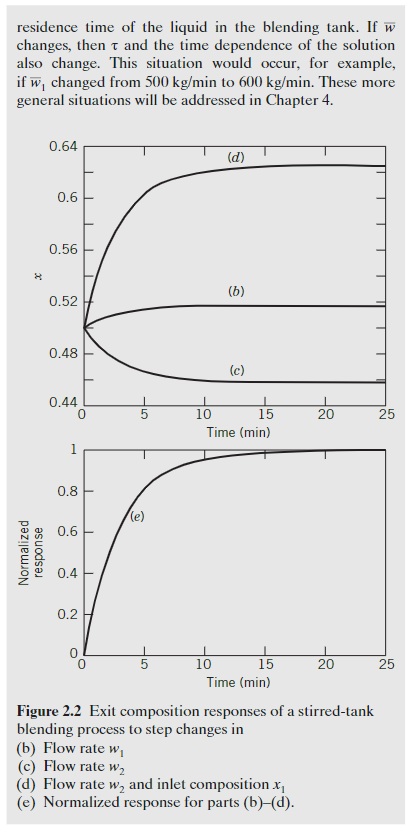
2.10 Example 2.1 plots responses for changes in input flows for the stirred tank blending system. Repeat part (b) and plot it. Next, relax the assumption that V is constant, and plot the response of x(t) and V(t) for the change in w1 for t=0 to 15 minutes. Assume that w2 and w remain constant. EXAMPLE 2.1 A stirred-tank blending process with a constant liquid holdup of 2m3 is used to blend two streams whose densities are both approximately 900kg/m3. The density does not change during mixing. (a) Assume that the process has been operating for a long period of time with flow rates of w1=500kg/min and w2=200kg/min, and feed compositions (mass fractions) of x1=0.4 and x2=0.75. What is the steadystate value of x ? (b) Suppose that w1 changes suddenly from 500 to 400kg/min and remains at the new value. Determine an expression for x(t) and plot it. (c) Repeat part (b) for the case where w2 (instead of w1 ) changes suddenly from 200 to 100kg/min and remains there. (d) Repeat part (c) for the case where x1 suddenly changes from 0.4 to 0.6 (in addition to the change in w2 ). (e) For parts (b) through (d), plot the normalized response xN(t), xN(t)=x()x(0)x(t)x(0) where x(0) is the initial steady-state value of x(t) and x() represents the final steady-state value, which is different for each part. SOLUTION (a) Denote the initial steady-state conditions by x,w, and so on. For the initial steady state, Eqs. 2-4 and 2-5 are applicable. Solve Eq. 2-5 for x : x=ww1x1+w2x2=700(500)(0.4)+(200)(0.75)=0.5 (b) The component balance in Eq. 2-3 can be rearranged (for constant V and ) as dtdx+x=ww1x1+w2x2x(0)=x=0.5 where V/w. In each of the three parts, (b)-(d), =3min and the right side of Eq. 2-19 is constant for this example. Thus, Eq. 2-19 can be written as 3dtdx+x=Cx(0)=0.5 where Cww1x1+w2x2 The solution to Eq. 2-20 can be obtained by applying standard solution methods (Kreyszig, 2011): x(t)=0.5et/3+C(1et/3) For case (b), C=600kg/min(400kg/min)(0.4)+(200kg/min)(0.75)=0.517 Substituting C into Eq. 2-22 gives the desired solution for the step change in w1 : x(t)=0.5et/3+0.517(1et/3) (c) For the step change in w2, C=600kg/min(500kg/min)(0.4)+(100kg/min)(0.75)=0.458 and the solution is x(t)=0.5et/3+0.458(1et/3) (d) Similarly, for the simultaneous changes in x1 and w2, Eq. 2-21 gives C=0.625. Thus, the solution is x(t)=0.5et/3+0.625(1et/3) (e) The individual responses in Eqs. 2-22-2-24 have the same normalized response: x()x(0)x(t)x(0)=1et/3 The responses of (b)-(e) are shown in Fig. 2.2. The individual responses and normalized response have the same time dependence for cases (b) (d) because =V/w=3 min for each part. Note that is the mean residence time of the liquid in the blending tank. If w changes, then and the time dependence of the solution also change. This situation would occur, for example, if w1 changed from 500kg/min to 600kg/min. These more general situations will be addressed in Chapter 4. Figure 2.2 Exit composition responses of a stirred-tank blending process to step changes in (b) Flow rate w1 (c) Flow rate w2 (d) Flow rate w2 and inlet composition x1 (e) Normalized response for parts (b)-(d)