i just posted and this code doesnt still doesnt work, now its giving me a syntax error on line 62 after fixing line 50. if there is more to it please elaborate because inputting n=random.getrandbits(len) was not the only fix.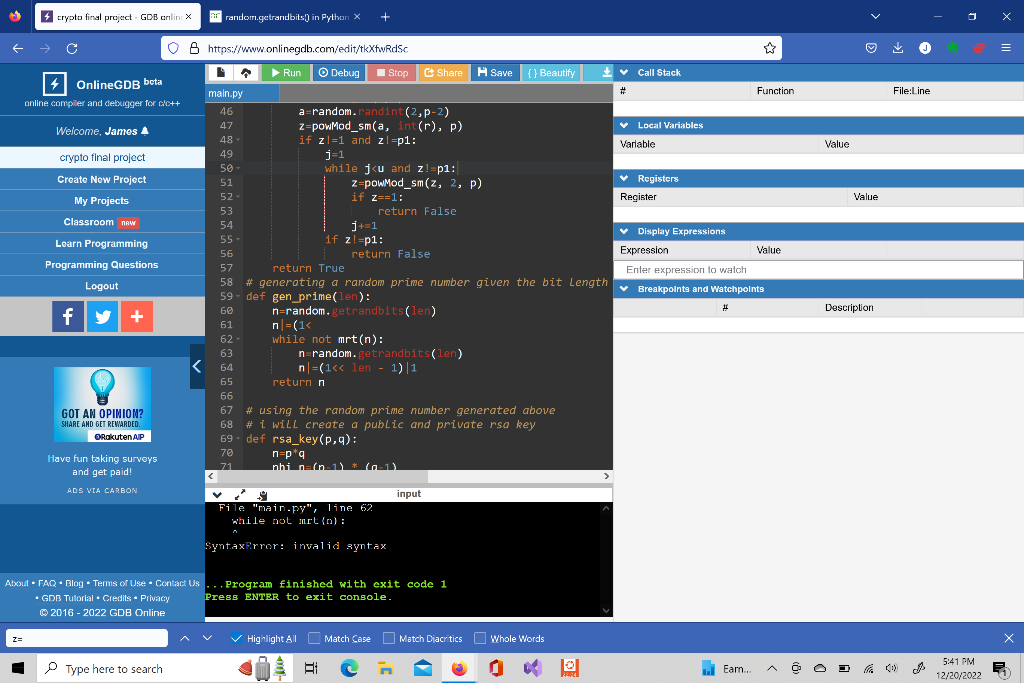

import random

def powMod_sm(base, exp, n):

exp_b=bin(exp)

value=base

for i in range(3, len(exp_b)):

value=(value**2)%n

if exp_b[i:i+1]=='1: ':

value = (value * base)% n

return value

# using the euclidean Algorithm

def computeGCD(x, y):

while y:

x, y = y, x % y

return x

#Extended euclidean Algorithm method to calculate gcd and get the coefficient

def extendedGCD(a, b):

if a == 0:

return b, 0, 1

gcd, x1, y1 = extendedGCD(b % a, a)

x = y1 - (b // a)* x1

y = x1

return gcd, x, y

# calculating the modular inverse using EEA

def mod_Inv(b, n):

gcd, _, t = extendedGCD(n, b)

if gcd==1:

i = t % n

elif gcd!=1:

print("Inverse is undefined")

return i

#miller-rabin Primality test

def mrt(p):

if p == 2 or p == 3:

return True

if p

return False

p1=p-1

t=15

u=0

r=p1

while r%2==0:

u=u+1

r=r/2

for i in range (1,t):

a=random.randint(2,p-2)

z=powMod_sm(a, int(r), p)

if z!=1 and z!=p1:

j=1

while j

z=powMod_sm(z, 2, p)

if z==1:

return False

j+=1

if z!=p1:

return False

return True

# generating a random prime number given the bit length

def gen_prime(len):

n=random.getrandbits(len)

n|=(1

while not mrt(n):

n=random.getrandbits(len)

n|=(1

return n

# using the random prime number generated above

# i will create a public and private rsa key

def rsa_key(p,q):

n=p*q

phi_n=(p-1) * (q-1)

for i in range (2,124):

if computeGCD(i, phi_n)==1:

e=i

break

d=mod_Inv(e,phi_n)

return n,e,d

# running main function and generating two prime number that are not =

def main():

p=gen_prime(60)

q=gen_prime(60)

while p==q:

q=gen_prime(60)

print ("prime number 1 is: ", p)

print ("prime number 2 is: ", q)

#generating private and public key

n,e,d=rsa_key(p,q)

print("public key is : ")

print("exponant e: ",e)

print("n : ", n )

print("private key is : ")

print("exponant d: ", d)

print("n : ", n)

#message to encrypt:

m= 8675390

print("The original message: ", m)

# encrypt using the powMod_sm method:

y=int(powMod_sm(m, e, n))

print("the encrypted message is: ", y)

#now decrypt the encrypted message using powMod_sm:

x=int(powMod_sm(y, int(d), n))

print("The original method after decryption: ", x)

main()