I need a solution in Excel

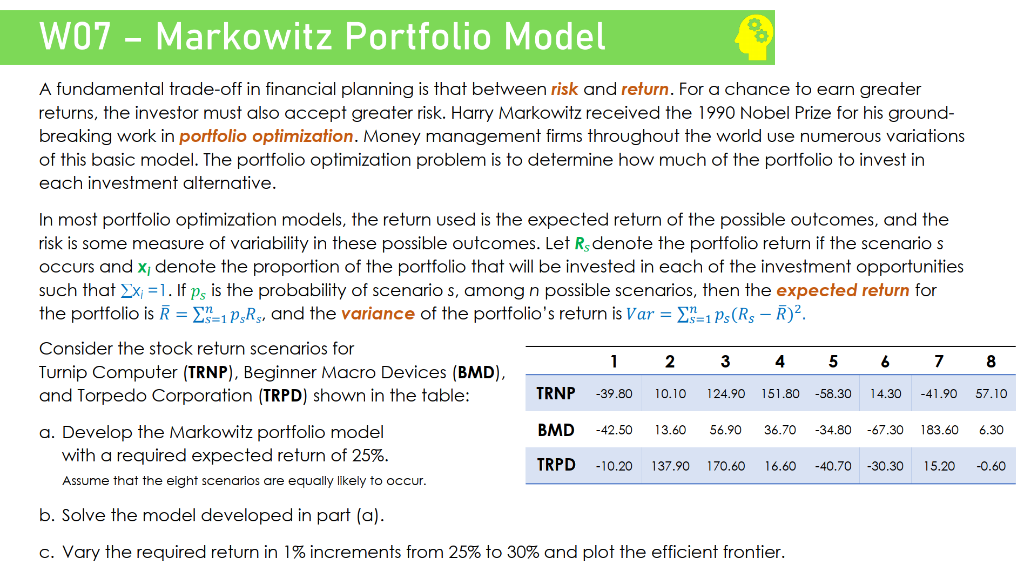
A fundamental trade-off in financial planning is that between risk and refurn. For a chance to earn greater returns, the investor must also accept greater risk. Harry Markowitz received the 1990 Nobel Prize for his groundbreaking work in porffolio optimization. Money management firms throughout the world use numerous variations of this basic model. The portfolio optimization problem is to determine how much of the portfolio to invest in each investment alternative. In most portfolio optimization models, the return used is the expected return of the possible outcomes, and the risk is some measure of variability in these possible outcomes. Let RS denote the portfolio return if the scenario s occurs and x1 denote the proportion of the portfolio that will be invested in each of the investment opportunities such that xi=1. If ps is the probability of scenario s, among n possible scenarios, then the expected return for the portfolio is R=s=1npsRs, and the variance of the portfolio's return is Var=s=1nps(RSR)2. Consider the stock return scenarios for Turnip Computer (TRNP), Beginner Macro Devices (BMD), and Torpedo Corporation (TRPD) shown in the table: a. Develop the Markowitz portfolio model with a required expected return of 25%. Assume that the elght scenarios are equally likely to occur. b. Solve the model developed in part (a). c. Vary the required return in 1% increments from 25% to 30% and plot the efficient frontier. A fundamental trade-off in financial planning is that between risk and refurn. For a chance to earn greater returns, the investor must also accept greater risk. Harry Markowitz received the 1990 Nobel Prize for his groundbreaking work in porffolio optimization. Money management firms throughout the world use numerous variations of this basic model. The portfolio optimization problem is to determine how much of the portfolio to invest in each investment alternative. In most portfolio optimization models, the return used is the expected return of the possible outcomes, and the risk is some measure of variability in these possible outcomes. Let RS denote the portfolio return if the scenario s occurs and x1 denote the proportion of the portfolio that will be invested in each of the investment opportunities such that xi=1. If ps is the probability of scenario s, among n possible scenarios, then the expected return for the portfolio is R=s=1npsRs, and the variance of the portfolio's return is Var=s=1nps(RSR)2. Consider the stock return scenarios for Turnip Computer (TRNP), Beginner Macro Devices (BMD), and Torpedo Corporation (TRPD) shown in the table: a. Develop the Markowitz portfolio model with a required expected return of 25%. Assume that the elght scenarios are equally likely to occur. b. Solve the model developed in part (a). c. Vary the required return in 1% increments from 25% to 30% and plot the efficient frontier