I need help correcting this problem:

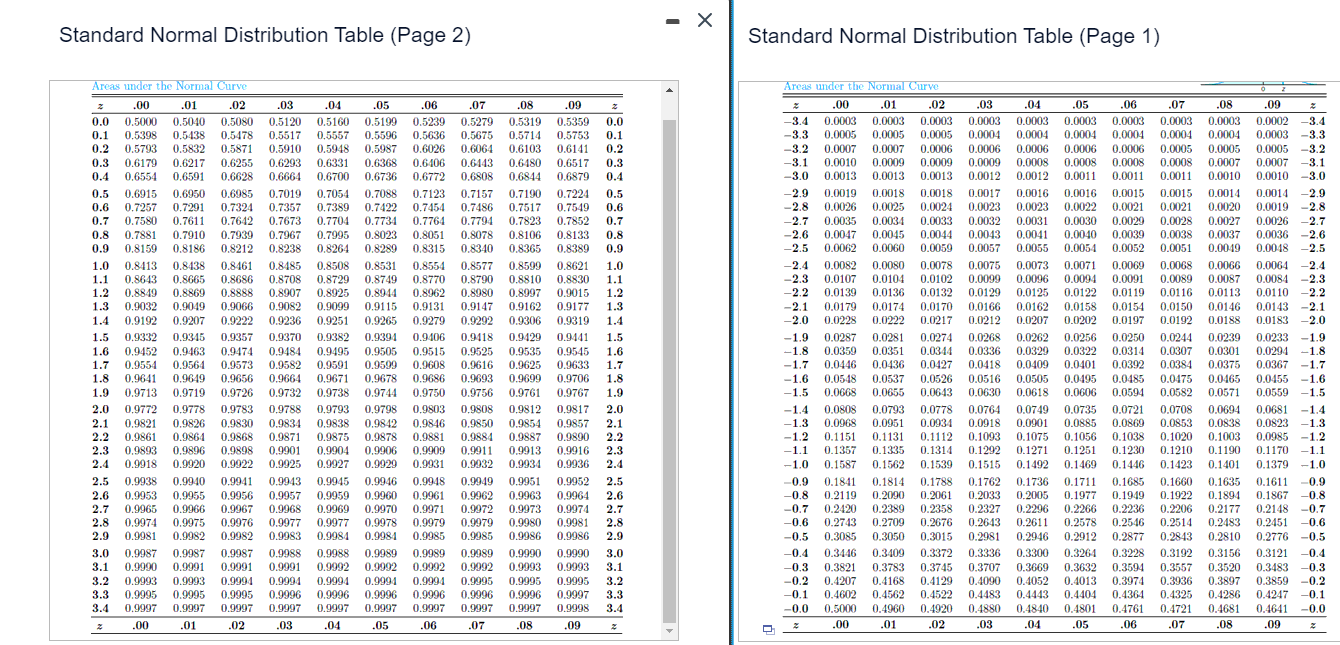
X Standard Normal Distribution Table (Page 2) Standard Normal Distribution Table (Page 1) Areas under the Normal Curve Areas under the Normal Curve 03 .04 .05 .06 .07 .08 09 .00 01 .02 .03 .04 .05 .06 .07 .08 .09 Z .00 .01 .02 -3.4 0.0003 0.0003 0.0003 0.0003 0.0003 0.0003 0.0003 0.0003 0.0003 0.0002 -3.4 0.0 0.5000 0.5040 0.5080 0.5120 0.5160 0.5199 0.5239 0.5279 0.5319 0.5359 0.0 -3,3 0.0005 0.0005 0.0005 0.0004 0.0004 0.0004 0.0004 0.0004 0.0004 0.0003 -3.3 0.1 0.5398 0.5438 0.5478 0,5517 0.5557 0,5596 0.5636 0,5675 0.5714 0.5753 0.1 0.5987 0.6026 0.6103 0.6141 0.2 -3.2 0.5910 0.5948 0.6064 0.0007 0.0007 0.0006 0.0006 0.0006 0.0006 0.0006 0.0005 0.0005 0.0005 -3.2 0.2 0.5793 0.5832 0.5871 -3.1 0.6331 0.6368 0.6406 0.6443 0.6480 0.6517 0.3 -3.1 0.0010 0.0009 0.0009 0.0009 0.0008 0.0008 0.0008 0.0008 0.0007 0.0007 0.3 0.6179 0.6217 0.6255 0.6293 -3.0 0.0013 0.0013 0.0013 0.0012 0.0012 0.0011 0.0011 0.0011 0.0010 0.0010 -3.0 0.4 0.6554 0.6591 0.6628 0.6664 0.6700 0.6736 0.6772 0.6808 0.6844 0.6879 0.4 -2.9 0.0019 0.0018 0.0018 0.0017 0.0016 0.0016 0.0015 0.0015 0.0014 0.0014 -2.9 0.5 0.6915 0.6950 0.6985 0.7019 0.7054 0.7088 0.7123 0.7157 0.7190 0.7224 0.5 -2.8 0.0026 0.0025 0.0024 0.0023 0.0023 0.0022 0.0021 0.0021 0.0020 0.0019 -2.8 0.6 0.7257 0.7291 0.7324 0.7357 0.7389 0.7422 0.7454 0.7486 0.7517 0.7549 0.6 0.7 -2.7 0.0035 0.0034 0.0033 0.0032 0.0031 0.0030 0.0029 0.0028 0.0027 0.0026 -2.7 0.7 0.7580 0.7611 0.7642 0.7673 0.7704 0.7734 0.7764 0.7794 0.7823 0.7852 0.8051 0.8078 0.8106 0.8133 0.8 -2.6 0.0047 0.0045 0.0044 0.0043 0.0041 0.0040 0.0039 0.0038 0.0037 0.0036 -2.6 0.8 0.7881 0.7910 0.7939 0.7967 0.7995 0.8023 0.8315 0.8340 0.8365 0.8389 0.9 -2.5 0.0062 0.0060 0.0059 0.0057 0.0055 0.0054 0.0052 0.0051 0.00-49 0.0048 -2.5 0.9 0.8159 0.8186 0.8212 0.8238 0.8264 0.8289 0.8599 0.8621 1.0 -2.4 0.0082 0.0080 0.0078 0.0075 0.0073 0.0071 0.0069 0.0068 0.0066 0.0064 -2.4 1.0 0.8413 0.8438 0.8461 0.8485 0.8508 0.8531 0.8554 0.8577 0.0096 0.0091 0.0089 0.0087 0.0084 -2.3 1.1 0.8643 0.8665 0.8686 0.8708 0.8729 0.8749 0.8770 0.8790 0.8810 0.8830 1.1 -2.3 0.0107 0.0104 0.0102 0.0099 0.0094 -2.2 0.0139 0.0136 0.0132 0.0129 0.0125 0.0122 0.0119 0.0116 0.0113 0.0110 -2.2 1.2 0.8849 0.8869 0.8888 0.8907 0.8925 0.8944 0.8962 0.8980 0.8997 0.9015 1.2 0.0146 0.0143 -2.1 1.3 0.9032 0.9049 0.9066 0.9082 0.9099 0.9115 0.9131 0.9147 0.9162 0.9177 1.3 -2.1 0.0179 0.0174 0.0170 0.0166 0.0162 0.0158 0.0154 0.0150 -2.0 0.0222 0.0217 0.0212 0.0207 0.0202 0.0197 0.0192 0.0188 0.0183 -2.0 1.4 0.9192 0.9207 0.9222 0.9236 0.9251 0.9265 0.9279 0.9292 0.9306 0.9319 1.4 0.0228 0.9418 0.9429 0.9441 1.5 -1.9 0.0287 0.0281 0.0274 0.0268 0.0262 0.0256 0.0250 0.0244 0.0239 0.0233 -1.9 1.5 0.9332 0.9345 0.9357 0.9370 0.9382 0.9394 0.9406 -1.8 0.0359 0.0351 0.0344 0.0336 0.0329 0.0322 0.0314 0.0307 0.0301 0.0294 -1.8 1.6 0.9452 0.9463 0.9474 0.9484 0.9495 0.9505 0.9515 0.9525 0.9535 0.9545 1.6 -1.7 0.9573 0.9582 0.9591 0.9599 0.9608 0.9616 0.9625 0.9633 1.7 -1.7 0.0446 0.0436 0.0427 0.0418 0.0409 0.0401 0.0392 0.0384 0.0375 0.0367 1.7 0.9554 0.9564 0.0537 0.0516 0.0495 0.0465 -1.6 -1.6 0.0548 0.0526 0.0505 0.0485 0.0475 0.0455 1.8 0.9641 0,9649 0.9656 0.9664 0.9671 0.9678 0.9686 0.9693 0.9699 0.9706 1.8 0.0594 0.0582 0.0571 0.0559 -1.5 1.9 0.9713 0.9719 0.9726 0.9732 0.9738 0.9744 0.9750 0.9756 0.9761 0.9767 1.9 -1.5 0.0668 0.0655 0.0643 0.0630 0.0618 0.0606 0.9817 2.0 -1.4 0.0808 0.0793 0.0778 0.0764 0.0749 0.0735 0.0721 0.0708 0.0694 0.0681 -1.4 2.0 0.9772 0.9778 0.9783 0.9788 0.9793 0,9798 0.9803 0,9808 0,9812 0.0869 0.0853 0.0838 0.0823 -1.3 2.1 0.9821 0.9826 0,9830 0.9834 0.9838 0,9842 0.9846 0.9850 0.9854 0.9857 2.1 -1.3 0.0968 0.0951 0.0934 0.0918 0.0901 0.0885 -1.2 0.1151 0.1131 0.1112 0.1093 0.1075 0.1056 0.1038 0.1020 0.1003 0.0985 -1.2 2.2 0.9861 0.9864 0.9868 0.9871 0.9875 0.9878 0.9881 0.9884 0.9887 0.9890 2.2 0.9916 2.3 -1.1 0.1357 0.1335 0.1314 0.1292 0.1271 0.1251 0.1230 0.1210 0.1190 0.1170 -1.1 2.3 0.9893 0.9896 0.9898 0.9901 0.9904 0.9906 0.9909 0.9911 0.9913 0.9927 0.9929 0.9931 0.9932 0.9934 0.9936 2.4 -1.0 0.1587 0.1562 0.1539 0.1515 0.1492 0.1469 0.1446 0.1423 0.1401 0.1379 -1.0 2.4 0.9918 0.9920 0.9922 0.9925 0.1736 0.1711 0.1685 0.1660 0.1635 0.1611 -0.9 2.5 0.9938 0.9940 0.9941 0.9943 0.9945 0.9946 0.9948 0.9949 0.9951 0.9952 2.5 -0.9 0.1841 0.1814 0.1788 0.1762 -0.8 0.2119 0.2090 0.2061 0.2033 0.2005 0.1977 0.1949 0.1922 0.1894 0.1867 -0.8 2.6 0.9953 0.9955 0.9956 0.9957 0.9959 0.9960 0.9961 0.9962 0.9963 0.9964 2.6 0.9971 0.9972 0.9973 0.9974 2.7 -0.7 0.2420 0.2389 0.2358 0.2327 0.2296 0.2266 0.2236 0.2206 0.2177 0.2148 -0.7 2.7 0.9965 0.9966 0.9967 0.9968 0.9969 0.9970 0.2514 0.2483 0.2451 -0.6 2.8 0.9974 0.9975 0.9976 0.9977 0.9977 0.9978 0.9979 0.9979 0.9980 0.9981 2.8 -0.6 0.2743 0.2709 0.2676 0.2643 0.2611 0.2578 0.2546 0.9982 0.9983 0.9984 0.9984 0.9985 0.9985 0.9986 0.9986 2.9 -0.5 0.3085 0.3050 0.3015 0.2981 0.2946 0.2912 0.2877 0.2843 0.2810 0.2776 -0.5 2.9 0.9981 0.9982 0.9989 0.9989 0.9990 0.9990 3.0 0.4 0.3446 0.3409 0.3372 0.3336 0.3300 0.3264 0.3228 0.3192 0.3156 0.3121 -0.4 3.0 0.9987 0.9987 0.9987 0.9988 0.9988 0.9989 -0.3 0.3821 0.3783 0.3745 0.3707 0.3669 0.3632 0.3594 0.3557 0.3520 0.3483 -0.3 3.1 0.9990 0.9991 0.9991 0.9991 0.9992 0.9992 0.9992 0.9092 0.9093 0.9993 3.1 0.4013 0.3936 0.3897 0.3859 -0.2 3.2 0.9993 0.9993 0.9994 0.9994 0.9994 0.9994 0.9994 0.9995 0.9995 0.9995 3.2 -0.2 0.4207 0.4168 0.4129 0.4090 0.4052 0.3974 0.4483 0.4443 0.4404 0.4364 0.4325 0.4286 0.4247 -0.1 3.3 0.9995 0.9995 0.9995 0.9996 0.9996 0.9996 0.9996 0.9996 0.9996 0.9997 3.3 -0.1 0.4602 0.4562 0.4522 0.9997 0.9997 0.9997 0.9997 0.9998 3.4 -0.0 0.5000 0.4960 0.4920 0.4880 0.4840 0.4801 0.4761 0.4721 0.4681 0.4641 -0.0 3.4 0.9997 0.9997 0.9997 0.9997 0.9997 .00 .01 .02 .03 .04 .05 .06 .07 .08 .09 .00 .01 .02 03 04 .05 .06 07 .08 .09A random sample of size 49 is taken from a normal population having a mean of 75 and a standard deviation of 4. A second random sample of size 25 is taken from a different normal population having a mean of 65 and a standard deviation of 3. Find the probability that the sample mean computed from the 49 measurements will exceed the sample mean computed from the 25 measurements by at least 8.2 but less than 10.7. Assume the difference of the means to be measured to the nearest tenth. Click here to view page 1 of the standard normal distribution table. Click here to view page 2 of the standard normal distribution table. The probability is 0.7845. (Round to four decimal places as needed.)