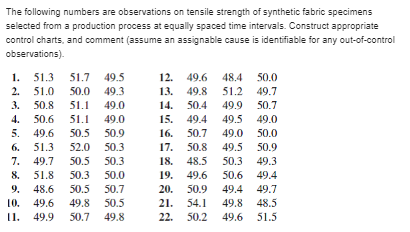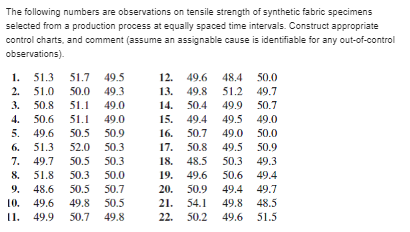
I need help

\fa. Show that another expression for the chi-squared statistic is N 2 Y = np jo Why is it more efficient to compute + using this formula? b. When the null hypothesis is (Hop, = P, = . . . = P: = 1/k (i.e., Pa = 1/k for all /), how does the formula of part (a) simplify? Use the simplified expression to cal- culate 12 for the pigeon/direction data in Exercise 4. Why is it more efficient to compute y" using this formula? b. When the null hypothesis is (Ho: p, = P2 =.... PA - 1/k (i.e., po 1/k for all ?). (i.e., for all i). how does the formula of part (3) simplify? Use the simplified expression to calculate y"for the pigeon/direction data in Exercise 4. Reference exercise 4 It is hypothesized that when homing pigeons are disoriented in a certain manner, they will exhibit no preference for any direction of flight after takeoff (so that the direction X should be uniformly distributed on the interval from 0' to 380*). To test this. 120 pigeons are disoriented, let loose, and the direction of flight of each is recorded; the resulting data follows. Use the chi-squared test at level .10 to see whether the data supports the hypothesis. Direction 0- .10. Would you use the one-sample t test to test hypotheses about the value of the true average ratio? Why or why not? Reference exercise 20 The article "Compatibility of Outer and Fusible Interlining Fabrics in Tailored Garments (Textile Res. J., 1997: 137-142) gave the following observations on bending rigidity (UN . m)for medium- quality fabric specimens, from which the accompanying Minitab output was obtained: (UN . m) Would you use a one-sample t confidence interval to estimate true average bending rigidity? Explain your reasoning.\fThe following numbers are observations on tensile strength of synthetic fabric specimens selected from a production process at equally spaced time intervals. Construct appropriate control charts, and comment (assume an assignable cause is identifiable for any out-of-control observations). 1. 51.3 51.7 49.5 12. 496 48.4 50.0 2. 51.0 50.0 49.3 13. 49.8 51.2 49.7 3. 50.8 51.1 4910 14. 50.4 49.9 50.7 4. 50.6 51.1 15. 49.4 49.5 49.0 5. 49.6 50.5 50.9 16. 50.7 49.0 50.0 51.3 52.0 50.3 17. 50.8 49.5 50.9 7. 49.7 50.5 50.3 18. 48.5 50.3 49.3 8. 51.8 50.3 50.0 19. 49.6 50.6 49.4 48.6 50.5 50.7 20. 50.9 49.4 49.7 10. 49.6 49.8 50.5 21. 54.1 49.8 48.5 11. 49.9 50.7 49.8 22. 50.2 49.6 51.5