I need help fixing this C++ code!!! Can somemone help finish the code I have made below to match the desired graphs mentioned in the assigment? I am new to c++ and need major help!

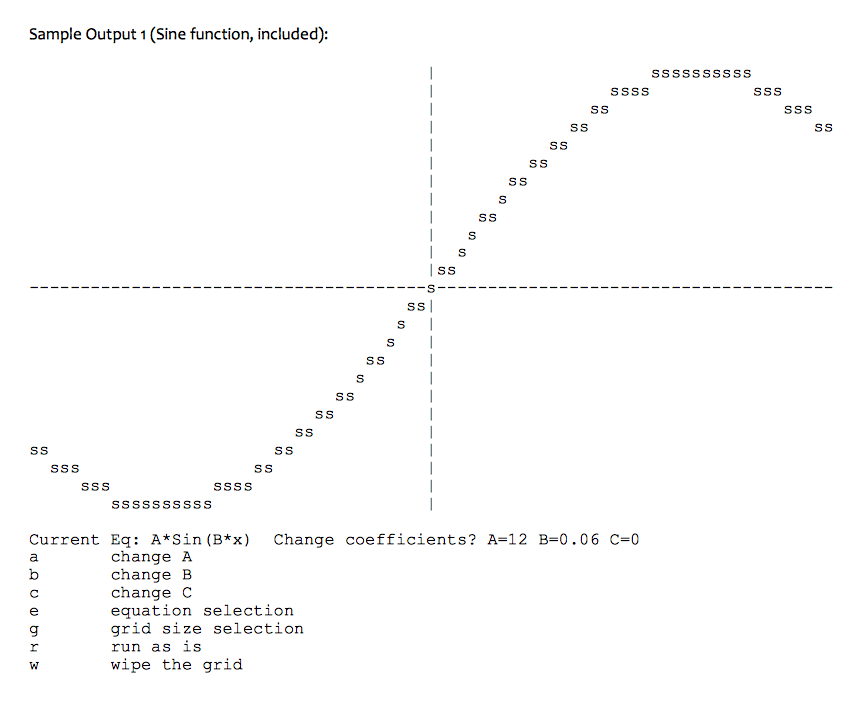
#include  #include  #include  using namespace std; // menu headers int menu_c(string&); int menu_e(int&, string&); int menu_g(string&); // function headers string grid_new(); void set_vars(int, int); void set_grid(string&); void grid_map(string&, int, int, char); void grid_map(string&, int, double, char); void grid_set_00 (string&, char); void grid_set_xax(string&, char); void grid_set_yax(string&, char); void grid_show(string&); void grid_res(string&); // gridable function headers // add additional gridable equation functionality here void eq_init(int, string&, bool, bool); void line_init(); void line_g(string&); void sin_init(); void sin_g(string&); // two sets of // global variables // for the grid int xmin= 0; int xmax= 0; int ymin= 0; int ymax= 0; // for the equations double a=1.0; double b=1.0; double c=1.0; string eq=""; // working portion of our project 2 starts here // don't mess with main() // // // int main() { set_vars(78, 24); // an X width by Y height grid string agrid = grid_new(); int doeq = 0; // active equation int doitem = 0; // flow control cout > menu_pic; switch(menu_pic) { case '0':doeq=0; eq_init(doeq,g,true,false); loop=false; break; case '1':doeq=1; eq_init(doeq,g,true,false); loop=false; break; case '2':doeq=2; eq_init(doeq,g,true,false); loop=false; break; case 'q':doitem=9 ; loop=false; break; default: cout  ymax) ; // out of bounds check else{ missing equation; g.replace(gcoor, 1, 1, c); }} // grid mapping with double to int type casting // we are function overloading here // is this necessary? or are we messing with you? // explain either way void grid_map(string& g, int x, double y, char c) { grid_map(g,x,static_cast(round(y)),c); } // equation specific global variable initialization // add additional equation functionality here void line_init() {eq="A*x +B" ; a = -1.00 ; b = -1.00; c = 0.00;} void sin_init() {eq="A*Sin(B*x)" ; a = 12.00 ; b = 0.06; c = 0.00;} // put the + at the center of the grid // don't mess with this void grid_set_00(string& g, char c) { grid_map(g, 0, 0, c); } // fill in the x axis void grid_set_xax(string& g, char c) { for(missing items){ grid_map(g, x, 0, c); }} // fill in the y axis void grid_set_yax(string& g, char c) { for(missing items){ grid_map(g, 0, y, c); }} // map the line function into the grid void line_g(string& g) { for(missing items){ double y = (a * x) + b; grid_map(g, x, y, '.'); }} // map the sin function into the grid void sin_g(string& g) { for(missing items){ double y = a * sin(b * x); grid_map(g, x, y, 's'); }} // define the limits of your grid // don't mess with this // what is the purpose of the lines with %2 ? void set_vars(int xsiz,int ysiz) { // out of bounds tests for x axis (max 100) if (xsiz%2!= 0) xsiz=xsiz+1; if (xsiz >100) xsiz= 100; // out of bounds tests for y axis (max 100) if (ysiz%2!= 0) ysiz=ysiz+1; if (ysiz >100) ysiz= 100; // align x=0,y=0 to the center xmin = -(xsiz/2); ymin = -(ysiz/2); xmax = +(xsiz/2); ymax = +(ysiz/2); } // menu for adjusting the equation coefficients // don't mess with this int menu_c(string& g) { int doitem = 1; bool loop = true; char menu_pic = ' '; while(loop) { cout > menu_pic; switch(menu_pic) { case 'a':cout  "; cin >> a; break; case 'b':cout  "; cin >> b; break; case 'c':cout  "; cin >> c; break; case 'e':doitem=4; loop=false; break; case 'g':doitem=5; loop=false; break; case 'r': loop=false; break; case 'q':doitem=9; loop=false; break; case 'w':grid_res(g); grid_show(g); break; default: cout > menu_pic; switch(menu_pic) { case 'x':cout  "; cin >> xsiz; break; case 'y':cout  "; cin >> ysiz; break; case 'r':set_vars(xsiz,ysiz); g=grid_new(); doitem=1; loop=false; break; case 'q':doitem=9; loop=false; break; default: cout   Project Simulated graphing of X,Y coordinates Overview: So far this semester we have spent lots of time working with do-while and while loops. This project's focus will be the For loop. We will spare you the effort of generating lots of code. Instead, we will provide you with what we call a skeleton This skeleton still has a lot of flesh on it's bones but is still DOA. The For loops will need something significant to work on, so we've selected the string data type to work with. You have been using strings since the very first lab and you really don't have any idea what you can do with them. Strings can be very large, so large that a single string can blow up memory, but we're not going to do that with this project. What we're going to do is simulate a graph with our string t's not really a graph so let's call it a string "grid". Your program, when you repair it, will put characters into an empty string. That string can then be cout'ed to the screen in a carefully ordered fashion so that your string grid simulates a graph. Now just putting characters into a string isn't all that challenging so you will have to make "gridable" functions that provide ordered pairs of numbers, coordinates, that will be converted into a single coordinate in the grid string This conversion is called a map. You will map a 2D system into a 1D system. Let's say the 2D system has x,y coordinate Your gridable function will take in x's and calculate corresponding y's. This makes x an independent variable and y a dependent variable. Your x's low value is the value at the left edge of the grid and your x's high value is the value at the right edge of the grid. The mapping function takes a set of these x,y pairs and maps a set of corresponding characters into the string. The string is then carefully cout'ed and will appear to have embedded within it the function of x and y. Of course a graph, and your grid, must have an origin. The origin of your grid is right in the middle of the simulated graph and will be identified by the character. Graphs also have axes. Since the origin is at the center, you will have a vertical y axis of characters, and a horizontal x axis of characters Everything in the skeleton is something that you have used in a lab, project or test with the exception of the string manipulators. There are three of them. The details of their usage and parameters can be found elsewhere in this document. The menu provided with the skeleton is fully functional but doesn't like invalid inputs very much. Last item t took a fair amount of time to originate this project. We hope you find it educational, entertaining and thought provoking. The volume of code that has been removed for breakage purposes is perhaps 160 characters. This is a thinking project as opposed to a coding project like project 1. When you "rediscover" the missing code do not share it with your fellow students. If you struggle with this, go to your GTA. Do not seek outside help C++ Objectives: In this project, we will explore some of the capabilities of the data types that we have been using this semester. In particular, we will practice working with: strings, for loops, driver programs, program tracing, arithmetic operators and call by reference parameters Tasks code, provided with this project, and repair it. The line numbers listed here are for Your goal is to take the broken c++ the unaltered original busted code There are a couple of questions embedded in the code that you will answer with comments embedded in your repaired code at the point in the code where the questions are asked. Those questions are found at lines 194 and 247 There is a simple formula to be reverse engineered at line 142. Another is missing at line 158. Two simple equations with missing formulas are at lines 173 and 174. You will need to derive the math equation needed to change 2D x,y coordinates into the 1D string coordinate system at line 188 need to fill in the missing parameters located at lines 143, 144, 145, 161, 162 and 163. there are more missing you W parameters at line 177 You will recreate the missing control logic of the for loops located at lines 159, 176, 218, 225, 232 and 240