I need help

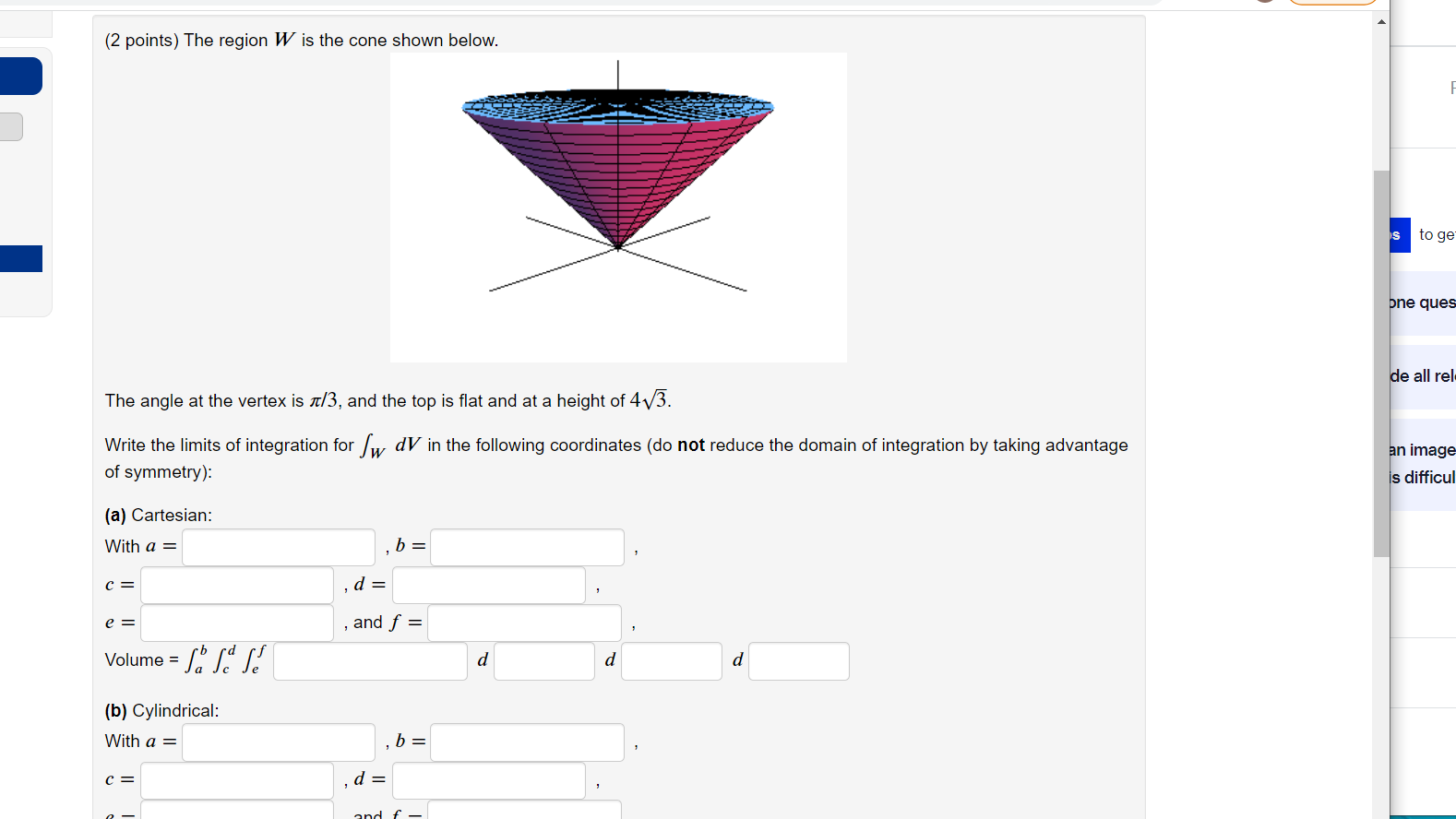
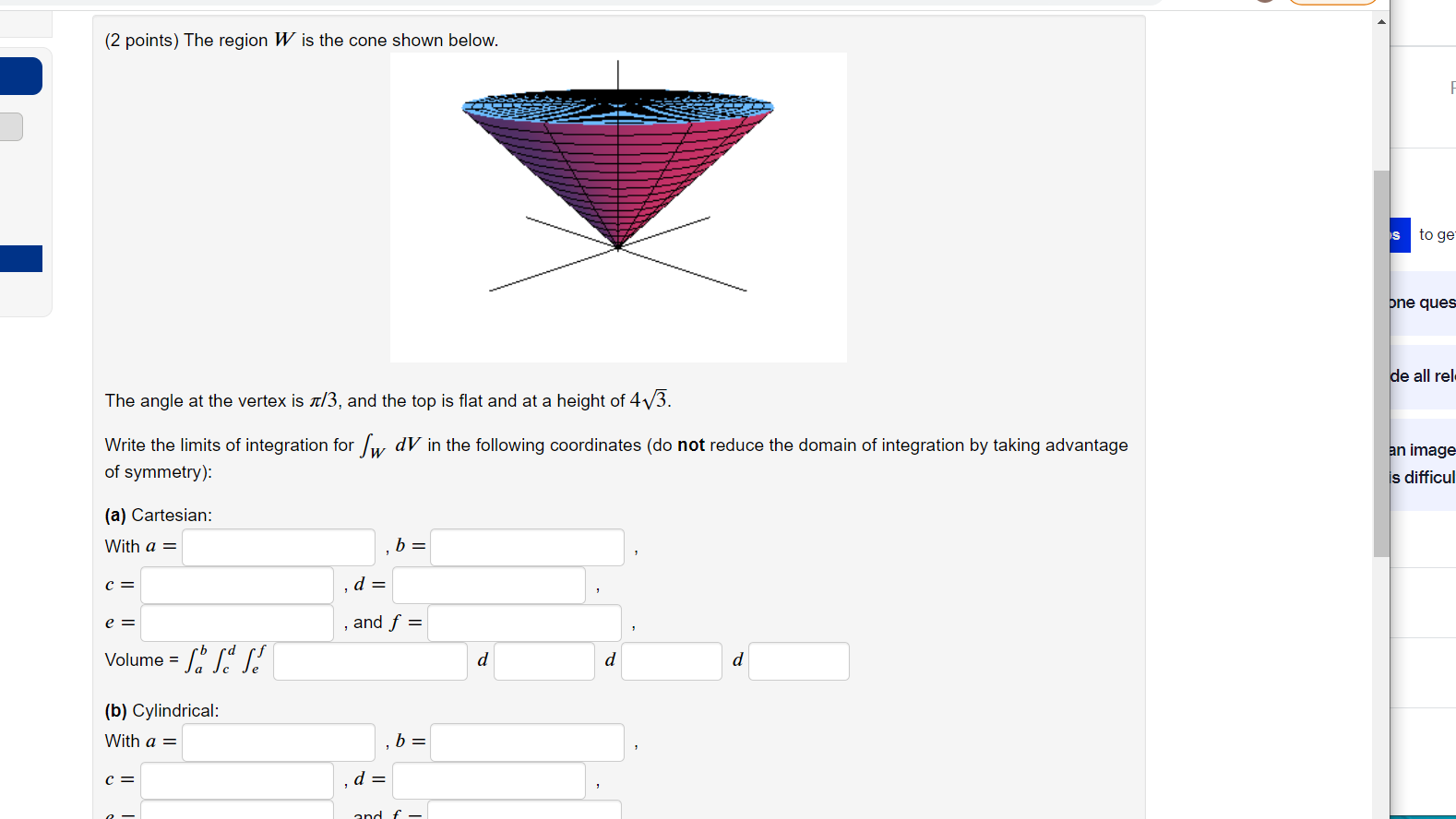
Homework8: Problem 2 Previous Problem Problem List Next Problem (1 point) Find the limits of integration ly, uy, Ix, ux, Iz, uz (some of which will involve variables x, y, z) so that Sit In " for axdizdy represents the volume of the region in the first octant that is inside the paraboloid y = x + z and between the planes y = 3 and y = 10. Ix = UX = Iz = UZ = ly = Uy = Note: You can earn partial credit on this problem. Preview My Answers Submit Answers You have attempted this problem 0 times. You have unlimited attempts remaining.Homework8: Problem 3 Previous Problem Problem List Next Problem (2 points) Suppose x, y, z) = .74:2 + y2 + 22 and W is the solid cylinder with height 5 and base radius 2 that is centered about the z-axis with its base at z = 2. Enter 9 as theta. (a) As an iterated integral, B D F de=f / / dza'rd A C E W with limits of integration (b) Evaluate the integral. (2 points) The region W is the cone shown below. The angle at the vertex is 1.7/3, and the top is at and at a height of 416. Write the limits of integration for [W (IV in the following coordinates (do not reduce the domain of integration by taking advantage ol symmetry): (a) Cartesian: Witha= ,b= . C= , = , e= ,andf: . Volume=LdeLf d d d (b) Cylindrical: With a = C: = 0 andf The angle at the vertex is 7/3, and the top is flat and at a height of 4v3. Write the limits of integration for w dl in the following coordinates (do not reduce the domain of integration by taking advantage of symmetry): (a) Cartesian: With a = b = d = e = and f = Volume = S ra fe d d d (b) Cylindrical: With a = , b= d = 2= , and f = Volume = Sa Je fe d d d (c) Spherical: With a = b = C= d = e = and f = Volume = S Je fe d d dHomework8: Problem 5 Previous Problem Problem List Next Problem (2 points) Write a triple integral including limits of integration that gives the volume of the cap of the solid sphere x2 + y2 + 22 S 20 cut off by the plane z = 2 and restricted to the rst octant. (In your integral, use theta, rho, and phi for 6, p and q, as needed.) What coordinates are you using? (Enter canesian, cylindrical, or spherical.) Witha= ,b= . C: a = : e= ,andf= . Volume=fjchf d d d Note: You can earn partial credit on this problem. Preview My Answers SubmitAnswers