I need help knowing how to answer question numbers 4,5,6,7,8,10,11, and 15

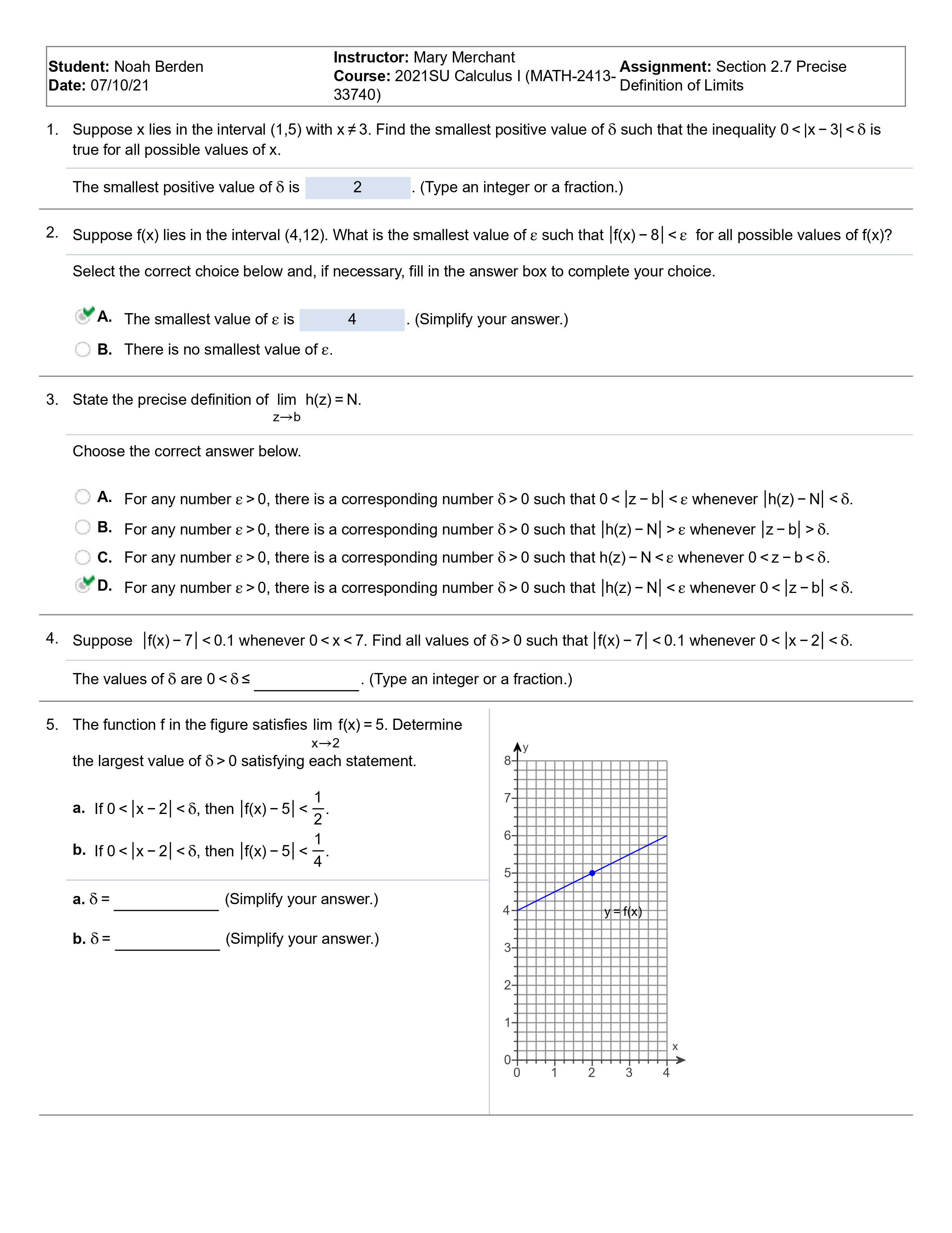
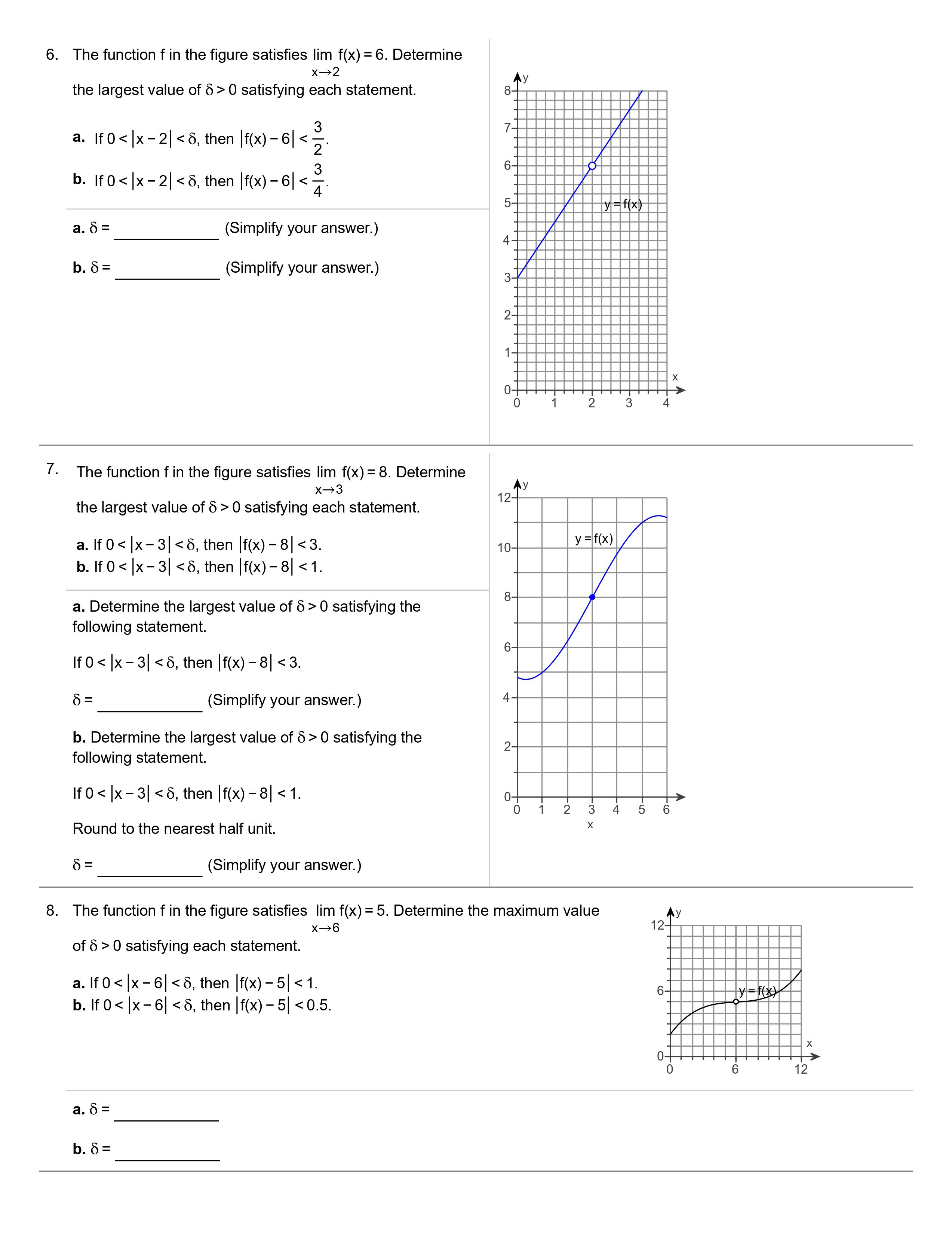
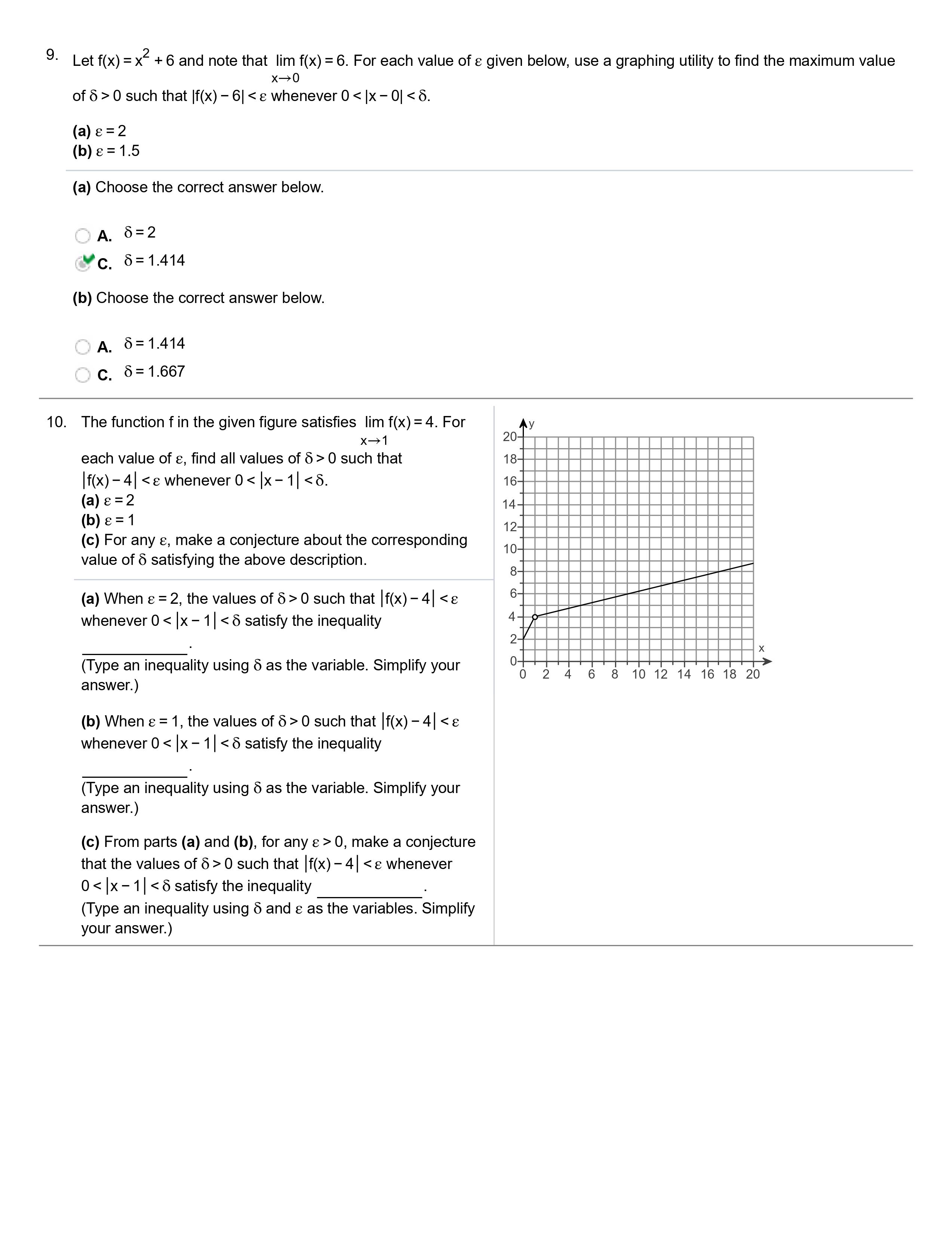
Student: Noah Berden Instructor: Mary Merchant Course: 2021SU Calculus I (MATH-2413- Assignment: Section 2.7 Precise Date: 07/10/21 33740) Definition of Limits 1. Suppose x lies in the interval (1,5) with x # 3. Find the smallest positive value of 8 such that the inequality 0 0, there is a corresponding number 8 > 0 such that 0 0, there is a corresponding number 8 > 0 such that [h(z) - N| > & whenever (z - b| > 6. C. For any number & > 0, there is a corresponding number 8 > 0 such that h(z) - N 0, there is a corresponding number 8 > 0 such that |h(z) - N| 0 such that |f(x) - 7| 0 satisfying each statement. a. If 0 . b. If 0 2 the largest value of 6 > 0 satisfying each statement. 3 a. If03 the largest value of 5 > 0 satisfying each statement. a. |f0 0 satisfying the following statement. IfO 0 satisfying the following statement. lf06 of 6 > 0 satisfying each statement. a. |f00 of 6 > 0 such that |f(x) 6| 1 each value of 8, nd all values of 6 > 0 such that |f(x) 4I 0 such that |f(x) 4| 0 such that If(x) 4| 0, make a conjecture that the values of 6 > 0 such that |f(x) 4| 0 such that X - 2 If(x) -4| 0, make a conjecture about the value of 8 that satisfies the preceding inequality. (a) When & = 1, the values of 8 > 0 such that |f(x) - 4| 0 such that |f(x) - 4| 0, make a conjecture that the values of 8 > 0 such that |f(x) - 4| 0 be given. Choose the correct proof below. O A. Choose 8 = 98. Then, |(9x - 5) - - 5| 0 be given. Choose the correct proof below. O A. Let 8 = 28. Then X2 - 64 X - 8 -16 0 - 7 0 satisfying the following statement. If(x) - 1| 0, find a corresponding value of 8 > 0 satisfying the following statement. X - 1 If(x)- 1 0. (Type an integer or a decimal.) b. For any & > 0, find a corresponding value of 8 > 0. Find an expression for 8 in terms of &. 16. We say that lim f(x) = co if for each positive number M, there is a corresponding N > 0 such that f(x) > M whenever x > N. X - OC X Use this definition to prove lim 140 -= 00 . X - 0o First find N, given M. Suppose M > 0 is given. Let N = 140M and assume x > N. Choose the correct next line of the proof. O A. See that if x > N, then 140 X B. See that if x > N, then 7 > M. X O C. See that if x > N, then X N, then x