I need help on Question Number 6 , but we need to use question 2.

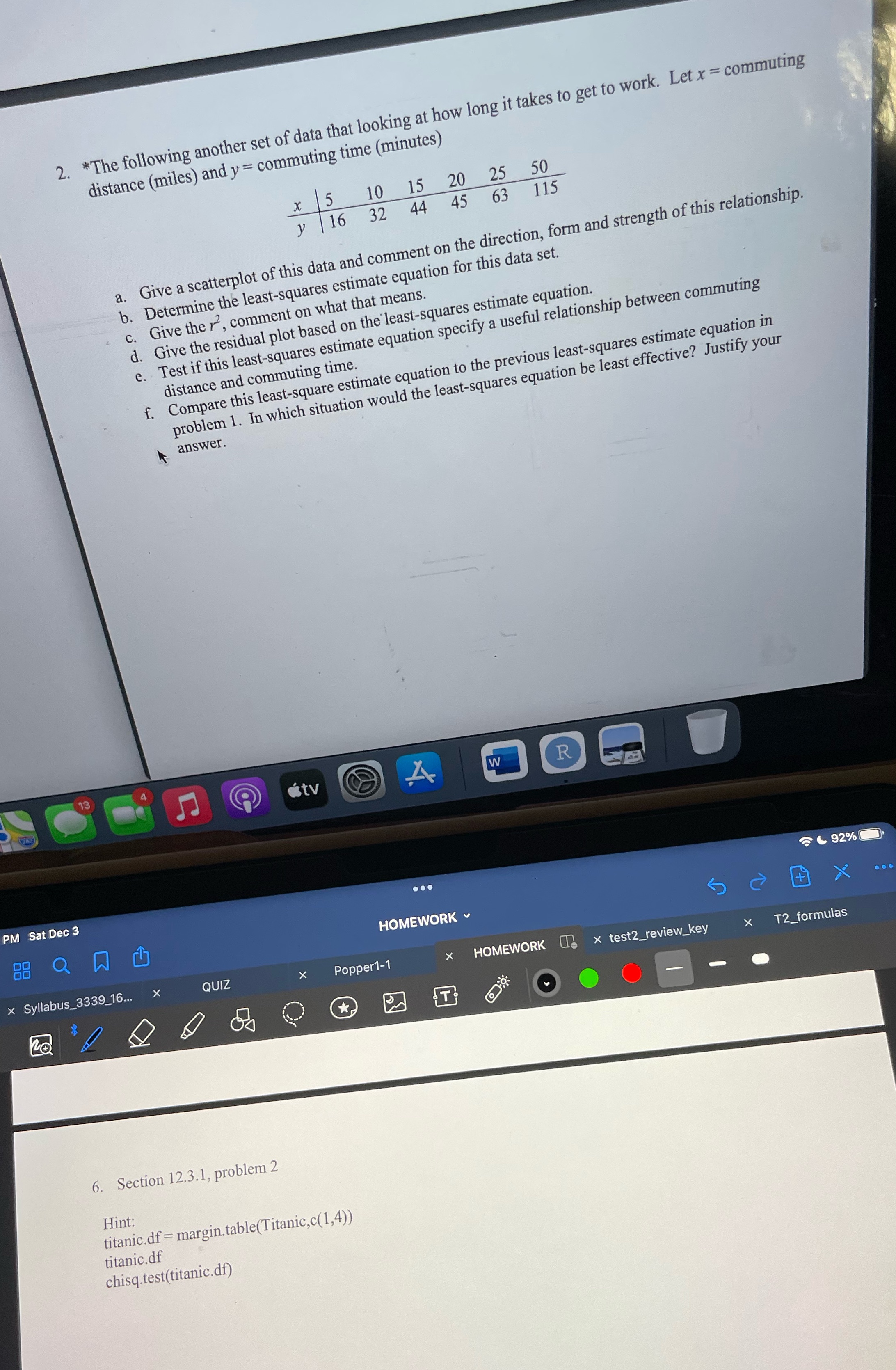
2. *The following another set of data that looking at how long it takes to get to work. Let x = commuting distance (miles) and y = commuting time (minutes) x 5 10 15 20 25 50 y 16 32 44 45 63 115 a. Give a scatterplot of this data and comment on the direction, form and strength of this relationship. b. Determine the least-squares estimate equation for this data set. c. Give the r, comment on what that means. d. Give the residual plot based on the least-squares estimate equation. Test if this least-squares estimate equation specify a useful relationship between commuting distance and commuting time. Compare this least-square estimate equation to the previous least-squares estimate equation in problem 1. In which situation would the least-squares equation be least effective? Justify your answer . 13 4 tv A w R PM Sat Dec 3 . . . - L 92% 88 Q HOMEWORK X . . . x Syllabus_3339_16... X QUIZ X Popper1-1 X HOMEWORK : x test2_review_key x T2_formulas 20 T. O O - 6. Section 12.3.1, problem 2 Hint: titanic.df = margin. table(Titanic,c(1,4)) titanic.df chisq.test(titanic.df)e. distance and commuting time. f. Compare this least-square estimate equation to the previous least-squares estimate cq problem 1. In which situation would the least-squares equation be least effective? Justify your answer. STRONG 80 POSITIVE LINEAR ProblemI would be least of feetive Br 40 20 smaller & appears to not be a relationship between distanced time. 20 30 40 50 b R- STUDIO Problem 2 1 distance seem to be significant to determine Call : I'm ( formula = 4 2 x ) time. Residual 3 4 2.58033 2.70820 3. 94672 - 5. 71 4 76 1.573 77 0.01637 coefficients. 7. 8 65 9 2. 8 760 2. 736 0.0521 2. 1423 0. 1132 18.930 4.590-05 * * * codes : . 00 ( * * ) 01* 1 . 05 . 0. 1 ' ' Error 4.034 on 4 degrees Multiple R- squared 0989, Equation : 4 = 7.8689 + 2. 142 3 x - R2 = 0- 989, about 28. 9 % the variation in time can be explained by this equation 20 40 60 100 HO BE = 0 4 HUB, to tots. = 18.930 pvalve = . 0000459 , reject null hypothesis . There evidence relationship beface distance of time using data re, Jay and Berk, Kenneth, Modern Mathematical Statistics with Applications, Thomson