I need help with answering a question which is

To find which strategies are dominated (strictly) in this game. Determine if there is any strategy for any player that is a dominant strategy for the player.

The question/game is as follows

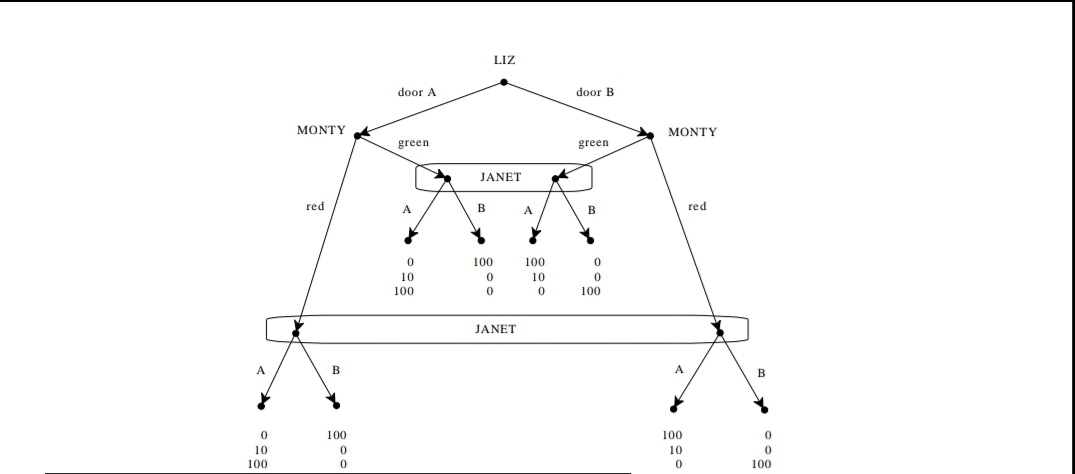
2. (a) The extensive form is shown on the next page. (b) The normal form is as follows (for Monty we go left to right, thus RG means 'Red if A and Green if B'; for Janet we go top to bottom, thus BA means 'B if Green and A if Red'). Monty Monty RR RG GR GG RR RG GR GG A 0, 10, 100 0,10,100 0, 10, 100 0, 10,100 Liz A 0, 10, 100 0,10, 100 100,0,0 100,0,0 Liz B 100, 10,0 100, 10,0 100, 10,0 100, 10,0 B 100,10,0 0,0,100 100, 10,0 0,0,100 Janet: AA Janet: BA Monty Monty RR RG GR GG RR RG GR GG Liz A 100,0,0 100,0,0 0, 10, 100 0, 10,100 Liz A 100,0,0 100,0,0 100,0,0 100,0,0 0,0, 100 100,10,0 0,0,100 100, 10,0 B 0,0,100 0,0,100 0,0,100 0,0,100 Janet: AB Janet: BB (c) There are two pure-strategy Nash equilibria: (A,RG,BA) and (A, GR,AB). (d) Since there are no proper subgames, the pure-strategy Nash equilibria coincide with the pure- strategy subgame-perfect equilibria. Hence there are two subgame-perfect equilibria: (A,RG,BA) and (A,GR,AB).\f2. [15 points] Consider the following game. Janet is a contestant in a popular game show and her task is to guess behind which door Liz, another contestant, is standing. With Janet out of the room, Liz chooses a door behind which to stand - either door A or door B. The host, Monty, observes this choice. Janet, not having observed Liz's choice, enters the room. Monty says to Janet either "Red cabbage" or "Green beans" (which sounds silly, of course, but it is as good as anything else you see on TV these days!). After hearing Monty's statement, Janet picks a door (says either "A" or "B"). If she picks the correct door, then she wins $100. If she picks the wrong door then she wins nothing. Liz wins $100 if Janet picks the wrong door and nothing if Janet picks the correct door. Thus, Liz would like to hide from Janet, while Janet would like to find Liz. What about Monty? Well, he likes the letter A. If Janet selects door A, then Monty gets $10, while if Janet selects door B then he gets nothing. (a) [6 points] Represent the game in extensive form. (b) [4 points] Write the corresponding normal (or strategic) form. Let Liz be the row player, Monty the column player and Janet the remaining player. (c) [3 points] Does this game have any pure-strategy Nash equilibria? If your answer is Yes, then name them. (d) [2 points] Does this game have any subgame-perfect equilibria? If your answer is Yes, then name them. If your answer is No, then explain why not