I need help with how to do each steps. Thanks.
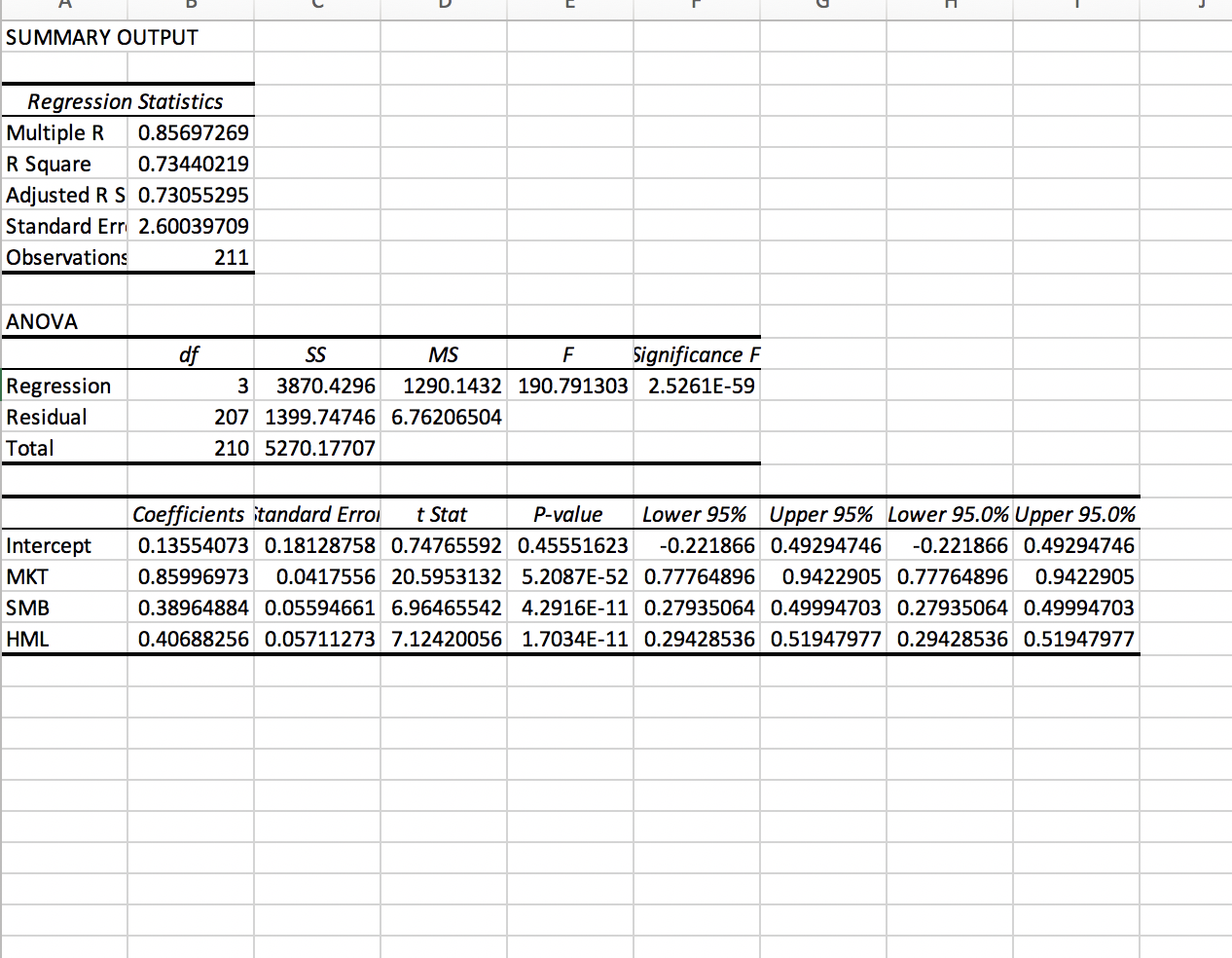
QUESTION 1 Click on this link to download the dataset in spreadsheet format that you are going to analyze. The first column represents the date, the second is the monthly percentage return of the Skyline Special Equities mutual fund (ticker:JASCX) and the remaining columns represent the US equity market return (MKT), Small-minus- Big (SMB), and High-minus-Low (HML) (see Ken French website for more details). The aim of this exercise is to use regression analysis to evaluate the exposure of the mutual fund returns to the risk factors (MKT, SMB, HML) and classify the style of the fund. The regression model is: mutual fund returns = alpha + beta1 * MKT + beta2 * SMB + beta3 * HML + error where the intercept alpha in the context of this model represents the risk-adjusted return and the slopes beta are the exposures of the mutual fund to the risk factors. Answer the following questions: The sign of the SMB coefficient indicates that the JASCX fund manager overweights - relative to the market factor - (type SMALL or LARGE) capitalization stocks while for HML the estimated coefficient indicates the manager overweights (type HIGH or LOW) Book-to-Market ratio stocks. Test the null hypothesis that the exposure of the fund to HML is equal to 0 against the alternative that it is different from 0 at the 1% significance level. Is the factor significant? (type YES or NO) Use the p-value of the intercept estimate (alpha) to test the one-sided hypothesis that alpha is less or equal to zero against the alternative that it is positive. Since the sign of the estimate of alpha is and the alternative hypothesis requires to reject the null hyp. for (type POSITIVE or NEGATIVE) values of alpha: does it matter how large the p-value is to decide to reject the null hypothesis? (type YES - if it matters- or NO - if it doesn't) Test the null hypothesis that the coefficient of MKT, beta1, is lower or equal to -1 against the alternative that it is larger. The test statistic for this hypothesis is and at 1% significance level we (type REJECT or DO NOT REJECT) the null hypothesis Test the overall significance of the regression model, that is, HO: beta1 = beta2 = beta3 = 0 against the alternative that at least one of the coefficients is different from zero. Calculate the F statistic for this hypothesis which is F distributed with 3 degrees of freedom in the numerator and 207 in the denominator. At 1% level the null hypothesis is (type REJECT or DO NOT REJECT)SUMMARY OUTPUT Regression Statistics Multiple R 0.85697269 R Square 0.73440219 Adjusted R S 0.73055295 Standard Err 2.60039709 Observations 211 ANOVA df SS MS F Significance F Regression 3 3870.4296 1290.1432 190.791303 2.5261E-59 Residual 207 1399.74746 6.76206504 Total 210 5270.17707 Coefficients itandard Errol t Stat P-value Lower 95% Upper 95% Lower 95.0% Upper 95.0% Intercept 0.13554073 0.18128758 0.74765592 0.45551623 -0.221866 0.49294746 -0.221866 0.49294746 MKT 0.85996973 0.0417556 20.5953132 5.2087E-52 0.77764896 0.9422905 0.77764896 0.9422905 SMB 0.38964884 0.05594661 6.96465542 4.2916E-11 0.27935064 0.49994703 0.27935064 0.49994703 HML 0.40688256 0.05711273 7.12420056 1.7034E-11 0.29428536 0.51947977 0.29428536 0.51947977