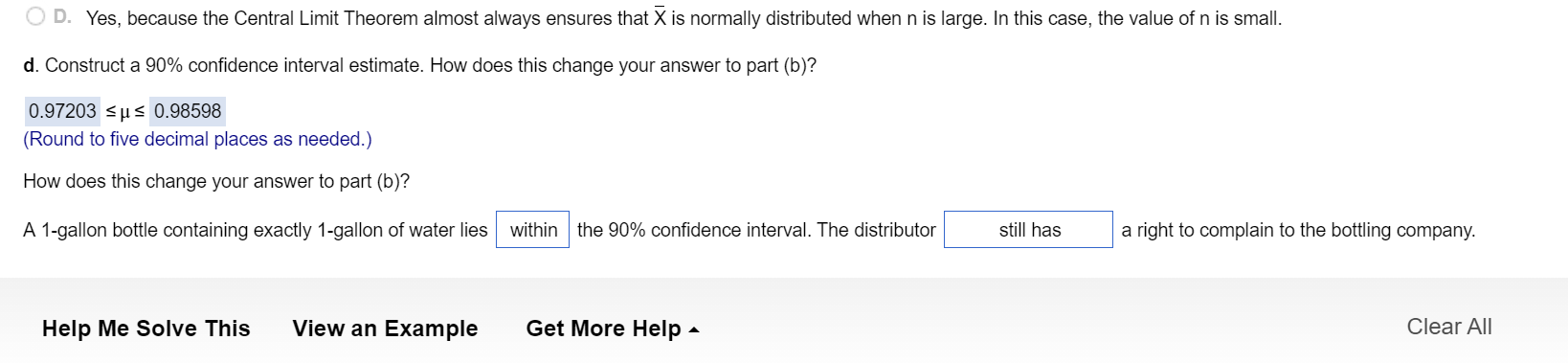
I need help with interpreting the confidence interval estimate in part D. How do I know when the population mean (Mu) lies within the 90% confidence level estimate that I calculated?

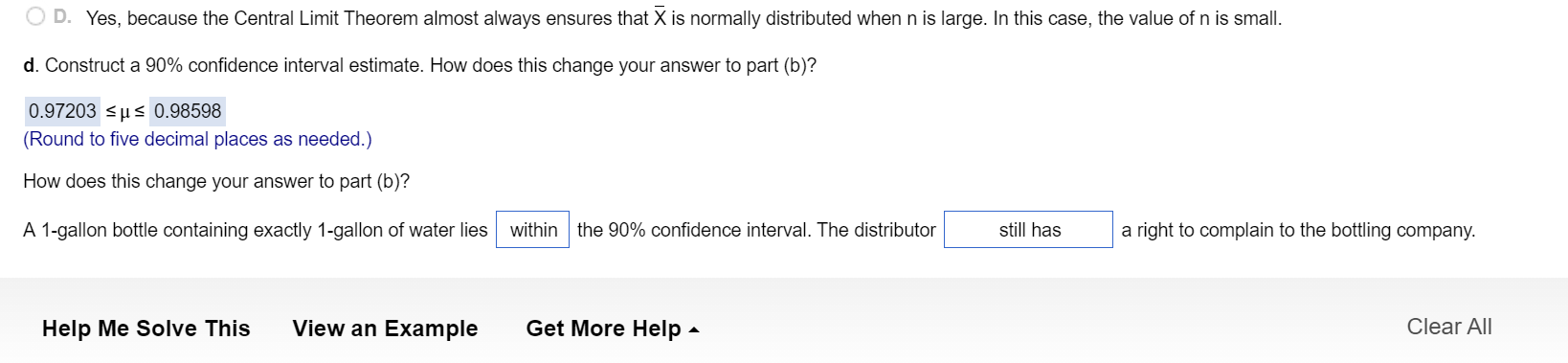
D.) A? 1-gallon bottle containing exactly? 1-gallon of water lies(within or outside)the ?90% confidence interval. The distributor(now does not have, still does not have, still has, now has) a right to complain to the bottling company.

In a survey of 3,990 adults concerning complaints about restaurants, 1,476 complained about dirty or ill-equipped bathrooms and 1,177 complained about loud or distracting diners at other tables. Complete p2 through ((2) below. 3. Construct a 95% condence interval estimate of the population proportion of adults who complained about dirty or ill-equipped bathrooms. 0.355 s 1: 5 0.385 (Round to four decimal places as needed.) b. Construct a 95% condence interval estimate of the population proportion of adults who complained about loud or distracting diners at other tables. 0.2809 5 155 0.3092 (Round to four decimal places as needed.) c. How would the manager of a chain of restaurants use the results of (a) and (b)? Which of the following is the best summary of the information derived from (a)? O A. The manager can be 95% condent that the sample proportion of all adults who complained about dirty or ill-equipped bathrooms lies within the intenral in (a). O B. There is a 95% probability that the sample proportion of all adults who complained about dirty or ill-equipped bathrooms lies within the interval in (a). O C. There is a 95% probability that the population proportion of all adults who complained about dirty or illequipped bathrooms lies within the interval in (a). D. The manager can be 95% condent that the population proportion of all adults who complained about dirty or illequipped bathrooms lies within the interval in (a). D. Yes. because the Central Limit Theorem almost always ensures that X is normally distributed when n is large. In this case, the value of n is small. :1. Construct a 90% confidence interval estimate. How does this change your answer to part (b)? 0.97203 5 p 5 0.98598 (Round to ve decimal places as needed.) How does this change your answer to part (b)? A 1-gallcn bottle containing exactly 1-gallcn of water lies Help Me Solve This View an Example within the 90% condence interval. The distributor Get More Help - still has a right to complain to the bottling company. Clear All