I need help with the questions in the last photo.
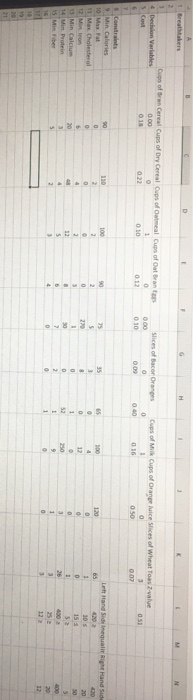
D 1 Breathtakers H N Cups of Bran Cereal Cups of Dry Cereal Cups of meal Cups of Oat brantes * Decision Variables 0.00 0 Cost 018 0.22 0.10 0.12 0.00 0.10 Slices of Bacer Oranges Cups of M Cups of Orange nice Slices of Wheat Toas-value 0 1 0 1 00 0.0 016 050 051 130 90 0 0 65 3 8 Constraints 9 Min. Calories 10 Mat 11 Max Cholesterol 12 Min from 1 Min Calcium 14 in Protein 15 Min be 16 120 0 100 2 . 2 12 S 50 2 0 3 3 4 12 22 1 4 30 3 5 0 0 2 0 1 52 1 1 Left Hand Sidequalit Right Hand Side 65 202 1 10 20 0 15 5 1 52 26 3 3 122 12 0 1 1 3R2R 250 9 18 20 Min Z-0.18x1 + 0.22x2 + 0.10x3 +0.12x4+ 0.10x5 +0.09x6 + 0.40x7 +0.16x8+0.50x9 + 0.07x10 s.t. (Min. Calories) 90x + 110x2 + 100x3 +90x4 + 75xs +35x6 + 65x7 + 100x8 + 120x9 + 65x10 2 420 (Max. Fat) 2x2 + 2x3 + 2x4 + 5x + 3x6 + 4x8 + 1x10 s 20 (Max. Cholesterol) 270x5 + 8x6 + 12x8 S 30 (Min. Iron) 6x1 + 4x2 + 2x3 + 3x4 + 1xs + 1x7 + 1x1025 (Min. Calcium) 20x1 +48x2 + 12x3 + 8x4 + 30xs +52x7 + 250x + 3x9 +26x102 400 (Min. Protein) 3x2 + 4x2 + 5x3 + 6x4 + 7x + 2X6 + 1x7 + 9xg + 1x3 + 3x10 2 20 (Min. Fiber) 5x1 + 2x2 + 3x3 + 4x4 + 1x2 + 3x10 2 12 (Non-negativity)x, X2, X3, X4, X5, X6, X7, X3, X9, X10 20 Optimal z-value $ 0.51 Variable Value Constraint Slack/Surplus Dual Prices 0 0 Reduced Costs 0.087 0.102 0 0.030 0.020 0.056 Bran cereal Dry cereal Oatmeal Oat bran Egs Bacon 10.01 15.10 0 0 1.025 0 0 0 1 (Min amt of calories) 2 (Max amt of fat) 3 (Max amt of cholesterol) 4 (Min amt of iron) 0.02 0 0 0.00026 nited States) - ody - 12 A A Aa A E... ALI x x A.O.AL . 1 Normal T No Spac... Heading 1 Heading 2 Title Subtitle Font Paragraph Styles Optimal z-value $ 0.51 Variable Value Constraint Slack/Surplus 10.01 15.10 Dual Prices 0 0 Bran cereal Dry cereal Oatmeal Oat bran Egg Bacon Orange Milk Orange Juice Wheat toast 0 0 1.025 0 0 0 0 1.241 0 2.975 Reduced Costs 0.087 0.102 0 0.030 0.020 0.056 0.324 0 0.384 0 1 (Min amt of calories) 2 (Max amt of fat) 3 (Max amt of cholesterol) 4 (Min amt. of iron) 5 (Min. amt. of calcium) 6 (Min. amt of protein) 7 (Min. amt. of fiber) 0.02 0 5 0 0 0 0.00026 0 0.00032 0.00096 1 United States Range of Optimality Variable Bran cereal Dry cereal Oatmeal Oat bran Egg Bacon Orange Milk Orange Juice Wheat toast Lower Limit 0.09 0.12 0.06 0.09 0.08 0.03 0.08 0.09 0.12 0.07 Current Value 0.18 0.22 0.10 0.12 0.10 0.09 0.40 0.16 0.50 0.07 Upper Limit No Upper Limit No Upper Limit 0.10 No Upper Limit No Upper Limit No Upper Limit No Upper Limit 0.17 No Upper Limit 0.10 Font Paragraph F Styles . 1 2 - 3 4 4 1 5 1 6 Range of Feasibility Constraint 1 Min amt of calories) 2 (Max amt of fat) 3 (Max amt of cholesterol) 4 (Min amt. of iron) 5 (Min. amt. of calcium) 6 (Min. amt of protein) 7 (Min. amt. of fiber) Lower Limit 419 9.99 14.90 No Lower Limit Current Value 420 20 30 5 400 20 12 Upper Limit 540.8 No Upper Limit No Upper Limit 5.02 402.50 25.22 12.21 98 No Lower Limit 8.19 na- Ao A 2.A. 11 Normal 1 No Spac... Heading 1 Heading 2 Title Paragraph Styles 3 16 + 3. If you could increase the right-hand side of one of the seven constraints which one would you select and why? How much would you increase this constraint by and what would be the amount? Provide all proper supports to justify your answer. (Note: Do not resolve the problem but rather use your knowledge of sensitivity analysis to answer this question.) 4. Unfortunately, a recent global health outbreak has caused the price of food to increase. If Breathtakers deals with the same distributor, the coat of milk will increase by 0.005. What impact will this change have on the optimal solution (i.e., decision variables and objective function). Do not re-solve the problem but rather, utilize your knowledge of sensitivity analysis to arrive at the answer. 5. What would be the effect on the optimal solution of increasing the minimum calorie requirement for the breakfast to 500 calories? To 600 calories? 6. Increase the breakfast calorie requirement to 700 calories and reformulate the model to establish upper limits on the servings of each food item to what you think would be realistic and appetizing. Determine the solution for the reformulated model. D 1 Breathtakers H N Cups of Bran Cereal Cups of Dry Cereal Cups of meal Cups of Oat brantes * Decision Variables 0.00 0 Cost 018 0.22 0.10 0.12 0.00 0.10 Slices of Bacer Oranges Cups of M Cups of Orange nice Slices of Wheat Toas-value 0 1 0 1 00 0.0 016 050 051 130 90 0 0 65 3 8 Constraints 9 Min. Calories 10 Mat 11 Max Cholesterol 12 Min from 1 Min Calcium 14 in Protein 15 Min be 16 120 0 100 2 . 2 12 S 50 2 0 3 3 4 12 22 1 4 30 3 5 0 0 2 0 1 52 1 1 Left Hand Sidequalit Right Hand Side 65 202 1 10 20 0 15 5 1 52 26 3 3 122 12 0 1 1 3R2R 250 9 18 20 Min Z-0.18x1 + 0.22x2 + 0.10x3 +0.12x4+ 0.10x5 +0.09x6 + 0.40x7 +0.16x8+0.50x9 + 0.07x10 s.t. (Min. Calories) 90x + 110x2 + 100x3 +90x4 + 75xs +35x6 + 65x7 + 100x8 + 120x9 + 65x10 2 420 (Max. Fat) 2x2 + 2x3 + 2x4 + 5x + 3x6 + 4x8 + 1x10 s 20 (Max. Cholesterol) 270x5 + 8x6 + 12x8 S 30 (Min. Iron) 6x1 + 4x2 + 2x3 + 3x4 + 1xs + 1x7 + 1x1025 (Min. Calcium) 20x1 +48x2 + 12x3 + 8x4 + 30xs +52x7 + 250x + 3x9 +26x102 400 (Min. Protein) 3x2 + 4x2 + 5x3 + 6x4 + 7x + 2X6 + 1x7 + 9xg + 1x3 + 3x10 2 20 (Min. Fiber) 5x1 + 2x2 + 3x3 + 4x4 + 1x2 + 3x10 2 12 (Non-negativity)x, X2, X3, X4, X5, X6, X7, X3, X9, X10 20 Optimal z-value $ 0.51 Variable Value Constraint Slack/Surplus Dual Prices 0 0 Reduced Costs 0.087 0.102 0 0.030 0.020 0.056 Bran cereal Dry cereal Oatmeal Oat bran Egs Bacon 10.01 15.10 0 0 1.025 0 0 0 1 (Min amt of calories) 2 (Max amt of fat) 3 (Max amt of cholesterol) 4 (Min amt of iron) 0.02 0 0 0.00026 nited States) - ody - 12 A A Aa A E... ALI x x A.O.AL . 1 Normal T No Spac... Heading 1 Heading 2 Title Subtitle Font Paragraph Styles Optimal z-value $ 0.51 Variable Value Constraint Slack/Surplus 10.01 15.10 Dual Prices 0 0 Bran cereal Dry cereal Oatmeal Oat bran Egg Bacon Orange Milk Orange Juice Wheat toast 0 0 1.025 0 0 0 0 1.241 0 2.975 Reduced Costs 0.087 0.102 0 0.030 0.020 0.056 0.324 0 0.384 0 1 (Min amt of calories) 2 (Max amt of fat) 3 (Max amt of cholesterol) 4 (Min amt. of iron) 5 (Min. amt. of calcium) 6 (Min. amt of protein) 7 (Min. amt. of fiber) 0.02 0 5 0 0 0 0.00026 0 0.00032 0.00096 1 United States Range of Optimality Variable Bran cereal Dry cereal Oatmeal Oat bran Egg Bacon Orange Milk Orange Juice Wheat toast Lower Limit 0.09 0.12 0.06 0.09 0.08 0.03 0.08 0.09 0.12 0.07 Current Value 0.18 0.22 0.10 0.12 0.10 0.09 0.40 0.16 0.50 0.07 Upper Limit No Upper Limit No Upper Limit 0.10 No Upper Limit No Upper Limit No Upper Limit No Upper Limit 0.17 No Upper Limit 0.10 Font Paragraph F Styles . 1 2 - 3 4 4 1 5 1 6 Range of Feasibility Constraint 1 Min amt of calories) 2 (Max amt of fat) 3 (Max amt of cholesterol) 4 (Min amt. of iron) 5 (Min. amt. of calcium) 6 (Min. amt of protein) 7 (Min. amt. of fiber) Lower Limit 419 9.99 14.90 No Lower Limit Current Value 420 20 30 5 400 20 12 Upper Limit 540.8 No Upper Limit No Upper Limit 5.02 402.50 25.22 12.21 98 No Lower Limit 8.19 na- Ao A 2.A. 11 Normal 1 No Spac... Heading 1 Heading 2 Title Paragraph Styles 3 16 + 3. If you could increase the right-hand side of one of the seven constraints which one would you select and why? How much would you increase this constraint by and what would be the amount? Provide all proper supports to justify your answer. (Note: Do not resolve the problem but rather use your knowledge of sensitivity analysis to answer this question.) 4. Unfortunately, a recent global health outbreak has caused the price of food to increase. If Breathtakers deals with the same distributor, the coat of milk will increase by 0.005. What impact will this change have on the optimal solution (i.e., decision variables and objective function). Do not re-solve the problem but rather, utilize your knowledge of sensitivity analysis to arrive at the answer. 5. What would be the effect on the optimal solution of increasing the minimum calorie requirement for the breakfast to 500 calories? To 600 calories? 6. Increase the breakfast calorie requirement to 700 calories and reformulate the model to establish upper limits on the servings of each food item to what you think would be realistic and appetizing. Determine the solution for the reformulated model













