I need help with this program. Written in Java please

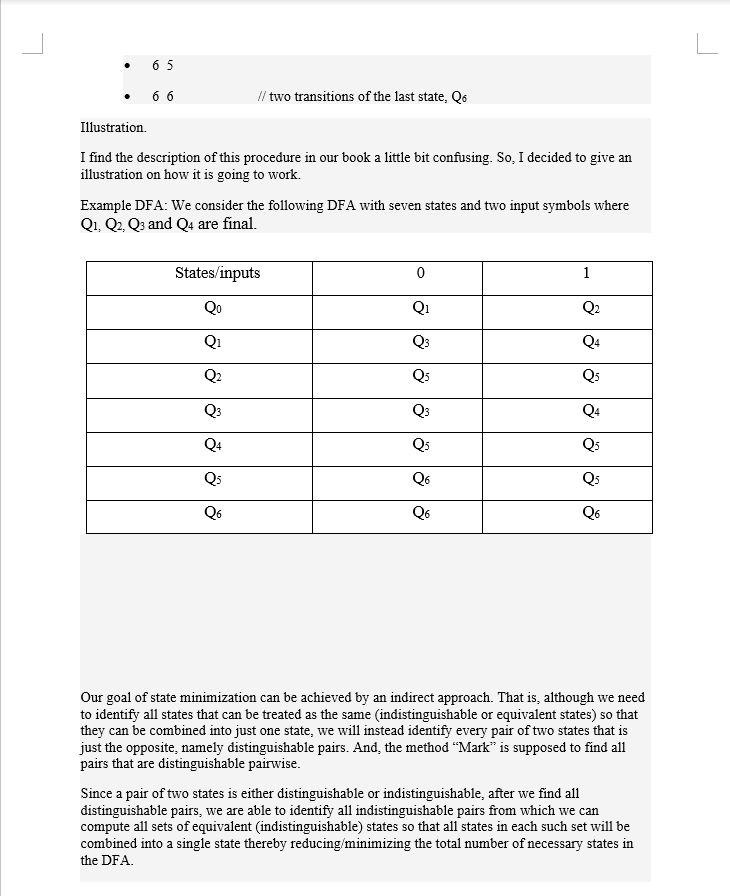
Program-2 DFA State Minimization Backgrounds Deterministic State Acceptors play many important roles in computing applications such as compiler design and regular language equivalence testing (the task of determining whether or not two regular languages are indeed the same despite their different looks). And, in certain cases, it is not only convenient but critical that they employ the minimum possible number of states Luckily, there are some simple and efficient procedures to reduce/minimize the number of states in a DFA such as methods "Mark" and "Reduce" on pages 67 and 69 of our textbook. Task: Write a program that computes and outputs all equivalent sets of indistinguishable states using the "Mark" method (page 67) of our textbook. Input DFA Use the Example DFA below in test-running your program. You can use following simplification assumptions to make the required input task relatively simple . States are numbered consecutively starting from 0 and state 0 is the Initial State Likewise input symbols are each one character long and are consecutively ordered such as * 0, 1,2,3, or a, b, c, d, .A DFA may have one or more number of states and zero or more number of Final states Under these simplifying assumptions, our input DFA can be completely specified by the following input frame: (Note comments are NOT parts of inputs) // total number of states // total number of Final states // two input symbols, 0 and 1 in that order // these are four Final states. So, the other three states are non-final. // two transitions of state 0, Qo // two transitions of state 1, Q1 // two transitions of state 2, Q2 // two transitions of the last state, Q6 Illustration. I find the description of this procedure in our book a little bit confusing. So, I decided to give an illustration on how it is going to work. Example DFA: We consider the following DFA with seven states and two input symbols where Q1, Q2, Qs and Q4 are final. States/inputs 0 Q4 Q5 Q4 Q5 Q6 Q6 Q5 Q6 Our goal of state minimization can be achieved by an indirect approach. That is, although we need to identify all states that can be treated as the same (indistinguishable or equivalent states) so that they can be combined into just one state, we will instead identify every pair of two states that is just the opposite, namely distinguishable pairs. And, the method "Mark" is supposed to find all pairs that are distinguishable pairwise Since a pair of two states is either distinguishable or indistinguishable, after we find all distinguishable pairs, we are able to identify all indistinguishable pairs from which we can compute all sets of equivalent (indistinguishable) states so that all states in each such set will be combined into a single state thereby reducing/minimizing the total number of necessary states in the DFA. 4. Since at least one additional distinguishable pair has been found during Iteartion-1, we will go ahead to the Iteration-2 Iteration-2 During this iteration, luckily we find no more distinguishable pair in this case. 6. We found a total of 18 distinguishable pairs. As there are 21 possible pairs out of seven states we have, there are a total of three indistinguishable pairs: They are: (q1, q3), (q2, q4) and (q5, q6). So, this example DFA has four classes of indistinguishable sets of states. They are (g0), (q1, q3), (42, q4) and (q5, q6). This is the expected outputs of your program. Note that the initial state q0 is not indistinguishable from any state, namely, it is not equivalent to any state we have or it is different from every other state. Program-2 DFA State Minimization Backgrounds Deterministic State Acceptors play many important roles in computing applications such as compiler design and regular language equivalence testing (the task of determining whether or not two regular languages are indeed the same despite their different looks). And, in certain cases, it is not only convenient but critical that they employ the minimum possible number of states Luckily, there are some simple and efficient procedures to reduce/minimize the number of states in a DFA such as methods "Mark" and "Reduce" on pages 67 and 69 of our textbook. Task: Write a program that computes and outputs all equivalent sets of indistinguishable states using the "Mark" method (page 67) of our textbook. Input DFA Use the Example DFA below in test-running your program. You can use following simplification assumptions to make the required input task relatively simple . States are numbered consecutively starting from 0 and state 0 is the Initial State Likewise input symbols are each one character long and are consecutively ordered such as * 0, 1,2,3, or a, b, c, d, .A DFA may have one or more number of states and zero or more number of Final states Under these simplifying assumptions, our input DFA can be completely specified by the following input frame: (Note comments are NOT parts of inputs) // total number of states // total number of Final states // two input symbols, 0 and 1 in that order // these are four Final states. So, the other three states are non-final. // two transitions of state 0, Qo // two transitions of state 1, Q1 // two transitions of state 2, Q2 // two transitions of the last state, Q6 Illustration. I find the description of this procedure in our book a little bit confusing. So, I decided to give an illustration on how it is going to work. Example DFA: We consider the following DFA with seven states and two input symbols where Q1, Q2, Qs and Q4 are final. States/inputs 0 Q4 Q5 Q4 Q5 Q6 Q6 Q5 Q6 Our goal of state minimization can be achieved by an indirect approach. That is, although we need to identify all states that can be treated as the same (indistinguishable or equivalent states) so that they can be combined into just one state, we will instead identify every pair of two states that is just the opposite, namely distinguishable pairs. And, the method "Mark" is supposed to find all pairs that are distinguishable pairwise Since a pair of two states is either distinguishable or indistinguishable, after we find all distinguishable pairs, we are able to identify all indistinguishable pairs from which we can compute all sets of equivalent (indistinguishable) states so that all states in each such set will be combined into a single state thereby reducing/minimizing the total number of necessary states in the DFA. 4. Since at least one additional distinguishable pair has been found during Iteartion-1, we will go ahead to the Iteration-2 Iteration-2 During this iteration, luckily we find no more distinguishable pair in this case. 6. We found a total of 18 distinguishable pairs. As there are 21 possible pairs out of seven states we have, there are a total of three indistinguishable pairs: They are: (q1, q3), (q2, q4) and (q5, q6). So, this example DFA has four classes of indistinguishable sets of states. They are (g0), (q1, q3), (42, q4) and (q5, q6). This is the expected outputs of your program. Note that the initial state q0 is not indistinguishable from any state, namely, it is not equivalent to any state we have or it is different from every other state