I need question 2 and the table that goes with it, but it seems i need to find the equation first, unsure what the equation is.

There is no other diagram, I uploaded the only thing that was on the page besides what I already have

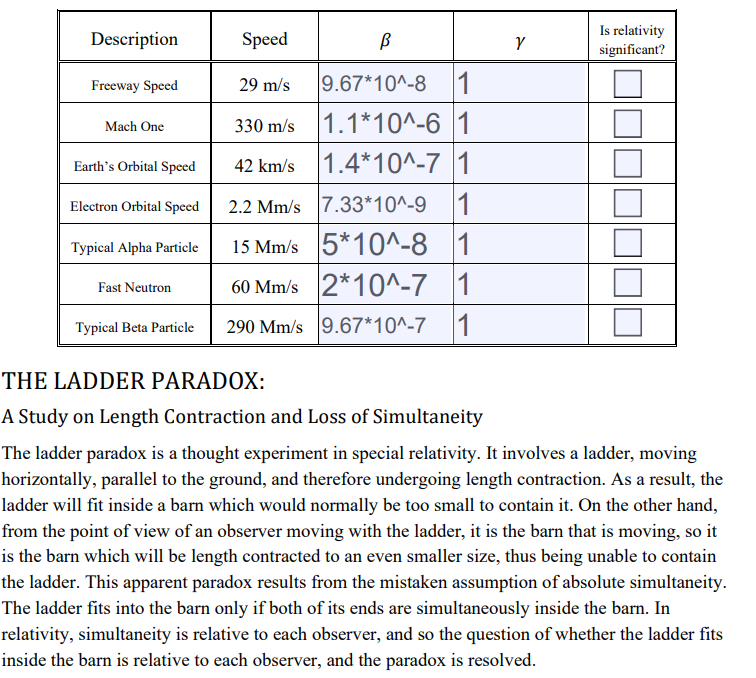
Description Speed B V Is relativity significant? Freeway Speed Mach One Earth's Orbital Speed Electron Orbital Speed 29 m/s 9.67*10^-8 1 330 m/s 1.1*10^-6 1 42 km/s 1.4*10^-7 1. 2.2 Mm/s 7.33*10^-9 1 15 Mm/s 5*10^-8 1 60 Mm/s 2*10^-7 1 290 Mm/s 9.67*10^-7 1 Typical Alpha Particle Fast Neutron Typical Beta Particle THE LADDER PARADOX: A Study on Length Contraction and Loss of Simultaneity The ladder paradox is a thought experiment in special relativity. It involves a ladder, moving horizontally, parallel to the ground, and therefore undergoing length contraction. As a result, the ladder will fit inside a barn which would normally be too small to contain it. On the other hand, from the point of view of an observer moving with the ladder, it is the barn that is moving, so it is the barn which will be length contracted to an even smaller size, thus being unable to contain the ladder. This apparent paradox results from the mistaken assumption of absolute simultaneity. The ladder fits into the barn only if both of its ends are simultaneously inside the barn. In relativity, simultaneity is relative to each observer, and so the question of whether the ladder fits inside the barn is relative to each observer, and the paradox is resolved. QUESTION 2: In the station's frame, at what time is the back of the ship located at the front of the station, tpp? At what time is the front of the ship at the back of the station, tfB? Which happens first? How much time is the ship fully inside the station, At = tfb - tbf? 7. Just for completeness, use Eqs. (11) and (6) (namely Xsh,B = Xst,B) to find the point BB. 8. Transfer your results to Table I. Table I Station Frame Ship Frame FF = (0 m, 0 s) FF' = (0 m, 0 s) FB = FB' = BF = BF' = BB = BB' At = At' = 3. Since the ship is travelling at a relativistic speed, it is length contracted. Use Eq. (1) to calculate the contracted length of the ship. Lsh = 320 m (numeric) (9) 4. The back of the ship travels at the same speed as the front of the ship, 180 m/us. However, at time t = 0 s, the back of the ship will be at x = -Lsh (i.e. this is the x-intercept). Create an equation that represents the motion of the back of the ship. Xsh,B = (symbolic) (10) Xsh,B (numeric) (11) a speed of B = 3/5 and the rest length of the station as Lst,o = 350 m. Clearly, if both are at rest, the ship will not fully fit into the station. To make the math a little easier, we note that c = 300 m/us. If we work in the units of meters and microseconds, we can avoid using scientific notation. Accordingly, the velocity is c = 180 m/us. Spaceship (USB Sent-Our-Prize, NCAA $17.01) Space-station (TBS-52, The Super Station) Back Front Front Back o o O O Lsh,0 = 400 m Lst,0 = 350 The easiest way to analyze this problem is to use a Minkowski Diagram, which is a plot of space (on the horizontal axis) vs. time (on the vertical axis). You will now make two Minkowski Diagrams, one in the frame of the space-station, and another in the frame of the spaceship. The Space-Station: 1. Since we consider the station as stationary, the front of the station will always be at zero and the back of the station will always be at 350 m. (F=Front, B =Back) Xst,F = 0 and Xst,B = Lst,0 (symbolic) (3) & (4) Xst,f = 0 m and Xst,B = 350 m (numeric) (5) & (6) These will correspond to two vertical lines on the Minkowski Diagram. Draw these lines on the plot area provided on the next page. Label these lines as Station - Front" and Station - Back. 2. The ship is travelling, as mentioned above, at 180 m/us. Accordingly, the motion of the front of the ship can be written as Xsh, F = ct (symbolic) (7) Xsh, F = 180 t (numeric) (8) This is assuming that the fronts of the ship and the station are located at x = 0 m at time t = 0 s. Draw the appropriate diagonal line representing the motion of the front of the ship, and label the line as Ship - Front. If you wish to draw this and the next line in a Description Speed B V Is relativity significant? Freeway Speed Mach One Earth's Orbital Speed Electron Orbital Speed 29 m/s 9.67*10^-8 1 330 m/s 1.1*10^-6 1 42 km/s 1.4*10^-7 1. 2.2 Mm/s 7.33*10^-9 1 15 Mm/s 5*10^-8 1 60 Mm/s 2*10^-7 1 290 Mm/s 9.67*10^-7 1 Typical Alpha Particle Fast Neutron Typical Beta Particle THE LADDER PARADOX: A Study on Length Contraction and Loss of Simultaneity The ladder paradox is a thought experiment in special relativity. It involves a ladder, moving horizontally, parallel to the ground, and therefore undergoing length contraction. As a result, the ladder will fit inside a barn which would normally be too small to contain it. On the other hand, from the point of view of an observer moving with the ladder, it is the barn that is moving, so it is the barn which will be length contracted to an even smaller size, thus being unable to contain the ladder. This apparent paradox results from the mistaken assumption of absolute simultaneity. The ladder fits into the barn only if both of its ends are simultaneously inside the barn. In relativity, simultaneity is relative to each observer, and so the question of whether the ladder fits inside the barn is relative to each observer, and the paradox is resolved. QUESTION 2: In the station's frame, at what time is the back of the ship located at the front of the station, tpp? At what time is the front of the ship at the back of the station, tfB? Which happens first? How much time is the ship fully inside the station, At = tfb - tbf? 7. Just for completeness, use Eqs. (11) and (6) (namely Xsh,B = Xst,B) to find the point BB. 8. Transfer your results to Table I. Table I Station Frame Ship Frame FF = (0 m, 0 s) FF' = (0 m, 0 s) FB = FB' = BF = BF' = BB = BB' At = At' = 3. Since the ship is travelling at a relativistic speed, it is length contracted. Use Eq. (1) to calculate the contracted length of the ship. Lsh = 320 m (numeric) (9) 4. The back of the ship travels at the same speed as the front of the ship, 180 m/us. However, at time t = 0 s, the back of the ship will be at x = -Lsh (i.e. this is the x-intercept). Create an equation that represents the motion of the back of the ship. Xsh,B = (symbolic) (10) Xsh,B (numeric) (11) a speed of B = 3/5 and the rest length of the station as Lst,o = 350 m. Clearly, if both are at rest, the ship will not fully fit into the station. To make the math a little easier, we note that c = 300 m/us. If we work in the units of meters and microseconds, we can avoid using scientific notation. Accordingly, the velocity is c = 180 m/us. Spaceship (USB Sent-Our-Prize, NCAA $17.01) Space-station (TBS-52, The Super Station) Back Front Front Back o o O O Lsh,0 = 400 m Lst,0 = 350 The easiest way to analyze this problem is to use a Minkowski Diagram, which is a plot of space (on the horizontal axis) vs. time (on the vertical axis). You will now make two Minkowski Diagrams, one in the frame of the space-station, and another in the frame of the spaceship. The Space-Station: 1. Since we consider the station as stationary, the front of the station will always be at zero and the back of the station will always be at 350 m. (F=Front, B =Back) Xst,F = 0 and Xst,B = Lst,0 (symbolic) (3) & (4) Xst,f = 0 m and Xst,B = 350 m (numeric) (5) & (6) These will correspond to two vertical lines on the Minkowski Diagram. Draw these lines on the plot area provided on the next page. Label these lines as Station - Front" and Station - Back. 2. The ship is travelling, as mentioned above, at 180 m/us. Accordingly, the motion of the front of the ship can be written as Xsh, F = ct (symbolic) (7) Xsh, F = 180 t (numeric) (8) This is assuming that the fronts of the ship and the station are located at x = 0 m at time t = 0 s. Draw the appropriate diagonal line representing the motion of the front of the ship, and label the line as Ship - Front. If you wish to draw this and the next line in a