i need this two papers

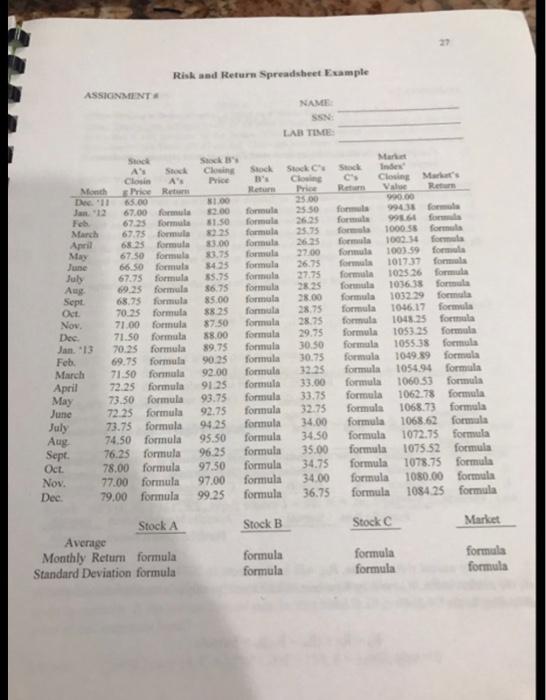
22 MODULE V: RISK AND RETURN INTRODUCTION To better understand the relationship between return and ris, we must know how return andre med tit. RATE OF RETURN If you buy at your pain or lose from that investment is called your return on investment. This return can be measured in two ways, in dollar tem or in percentage term. It is usually more convenient to summarize information about return in percentage term called rate of return. The rate of return is expressed as the change in value of an et plus any cash flows received during the period divided by the initial investment: R- P--P-P- PC P1 where R.- the actual rate of return during period, P-price (value) of asset at time - 1: P-price (value) of asset at time to cash flow roceived during the period from t-1 tot In the numerator of the above formula. Pe - Part is the capital gain or loss and is the dividend payment for a stock investment or interest payment for a bond investment. The first term on the right-hand side of the formula is called capital gains yield and the second term is called either dividend yield for a stock investment or current yield for a bond investment RISK The risk of concern to investors is the investment risk, which is related to the probability of low or negative returns. The greater the chance investors receive low returns, the riskier the investment. To quantify risk so that we can measure it, we generally deal with the probability distribution of rates of return. We can simply plot an investment's historical returns to construct a probability distribution. As the number of observations becomes large, say 60, the probability distribution will converge into a normal distribution, which has nice properties: (1) it is symmetrical around the mean; and (2) if you know both mean and standard deviation, you know all the distribution. Standard deviation is a statistical measure of the dispersion around the mean. The smaller the standard deviation, the tighter the probability distribution, and thus, the less risky the investment After computing rates of return for a time period, the mean and standard deviation of the eturn series can be calculated as follows: N ER- Mean (expected return) R - Standard Deviation N-1 Excel AVERAGE valuel, value2...) STDEV(value, value, ...) An asset's risk can be analyzed in two ways: (l) on a stand-alone basis, where the set is considered in isolation, and (2) in a portfolio context, where the set is included in a portfolio On a stand-alone basis. If an asset is not included in a portfolio, then standard deviation is its stand-alone risk, which is the risk that an investor would be exposed to Standard deviation measures the total risk of this asset. The smaller the standard deviation, the tighter the probability distribution, and accordingly, the lower the riskiness of the asset In a portfolio context. When an individual stock is held by itself, the risk measure is its standard deviation or total risk. Total risk, however, can be decomposed into two components: market risk and company specific risk. Market risk, or nondiversifiable risk, is the part of total risk that cannot be eliminated by diversification and stems from factors which systematically affoet most firms such as interest rate hikes, war, inflation, recessions, etc. On the other hand, company-specific risk, or diversifiable risk, is caused by such random events as lawsuits, strikes, and other events that are unique to a particular firm and it can be eliminated by proper diversification. Relevant risk. When investors are primarily concerned with portfolio risk rather than the risk of the individual securities in the portfolio, how should the riskiness of an individual stock be measured? One answer is provided by the Capital Asset Pricing Model (CAPM), which stipulates that there is a positive and linear relationship between a security's expected return and its systematic risk. In other words, the primary conclusion of the CAPM is that the relevant riskiness of an individual stock is its contribution to the riskiness of a well-diversified portfolio, or its market risk. Since market risk is the risk that remains after diversifying, it is inherent in the market and it can be measured by the degree to which a given stock tends to move or down with the market. CAPITAL ASSET PRICING MODEL (CAPM) ER)=R-f+IER)-RB where E(R) = the required rate of return on stock i; Ry the risk-free rate of return; E(R.) - the required rate of return on the market portfolio; and B - the beta coefficient of stock i. The beta of the market, Bu, is 1. 34 A mind why of a woman with the refund liebe couch which is of the Sovity wave that the stock bete officia de how the sockwffect the skiess of a diled portfolio, bestemor of 's risk Practically, the SAPS Index whose bisoul to one more them portfolio Irao be than 1 y 12, then this stock ve stock and is 30 per risker than the market wise, asock's be is less than 1. sy - then it is a defensivestock and is 40 perc less risky than the market To compute you must rely on historical return data. First, you need to collect past 60 monthly returns (five years of data of the stock and the overall market. Then, you regress the stock's returns against the market's returns in the following equation called the market model or the characteristie lines RE+BR where R stocki's return at time to the dependent variable of the regression R - market's retum at time to the independent variable of the regression - the constant term or the intercept of the regression: A -the beta coefficient of stock i or the slope of the regression; and the error term Using Excel to compute beta. Before using an analysis tool in Excel, you must arrange the data you want to analyze in columns of rows on your worksheet. This is your input range. The Data Analysis command is available in the Analysis group on the Data tab. If the Data Analysis command is not listed, you need to install the Analysis ToolPak in Microsoft Excel To install the Analysis ToolPak 1. Click File (on the top left corner) and then Option. Click Add-Ins and in the Add-Ins Inactive Application box, select the Analysis ToolPak check box, and then click GO next to the Manage box, and then click OK 3. After you load the Analysis ToolPak, the Data Analysis command is available in the Analysis group on the Data tab. SUMMARY OUTPUT Regression Statistics Multiple R 0.260823 0.068028 Adjusted R 0.025666 Square Standard Error 0.014815 R Square O ANOVA Regression Resid Total 01324 M 0.00015345057 0.000319 0.00035 0.00489 0.001 Upper repe X Variable 1 Car Se Lower 9 0.00359 0.00339967 0.0640 -0.00043 0.764330366 26723 0.21 0.29589 Lower 0309 -0.00042 -0.29589 Upper 95.0% 00136 1.2254 0.0136 1.2255 From the above output summary, the "Intercept" is a which equals 0.559% and the "X Variable is beta () which equals 0.76483. The beta of 0.76483 means that this stock is a defensive stock because its beta is less than the market beta of 1. When the market moves up (down) by 10 percent, this stock will move up (down) only 7.6483 percent PORTFOLIO RETURN AND BETA Once you compute ex post average returns and beta coeficients for all the stocks in the portfolio, you can compute the return on the portfolio, which is the weighted average of the individual stocks' returns, and the beta of the portfolio, which is the weighted average of the individual stocks" betas: N Rp = w;R,+W2R2+...+WnRN = w;R; and Bp = wiBi + W2B2+-+w.B- wiBi. where p = denotes portfolio; - the proportion of stock i relative to the portfolio's market value and the wi's must sum to 1; BA - the beta coefficient for stock i; and N w; = 1, which means that the sum of all proportions must equal 100 percent ZWI Risk and Return Exercisest Os January 2, 2014. you plan to invest $1.000.000 in three stocks to form a portfolio 5400.000 Stock A $200,000 in Stock Band 5400,000 in Stock C. To better se your portfoto's expected return and risk you decide to rely on the historical data of these three sing the past performance will be a good predictor for future performance. You have collected the monthly closing prices information for all three and the market index from December 2011 to December 2013 1. Create the spreadsheet and input the information given below. Next, calculate returns for each stock and the market index. All three stocks never pay dividends. Compute both mean and standard deviation of returns for all three stocks and the market index 2 Compute beta coefficients for all three stocks and report their respective regression ummary output. Next, calculate your portfolio's annual return and beta If the risk-free rate, nar, and the expected return on the market index, i, for 2014 will be 2 percent and 8 percent, respectively, what is your portfolio's required rate of return according to the CAPM? Month Dec. 2011 Jan 2013 Feb March April Mary June July Awe Sept Oct. Nov. Dec Jan. 2013 Feh March April May June July Aug Sept Oct Nov. Des Stock 65.00 67.00 67.25 67.75 68.25 67.50 66.50 67.75 69.25 68.75 70.25 71.00 71.50 70.25 69.75 71.50 72.25 73.50 72.25 73.75 74.50 76.25 78,00 77.00 79.00 Stock B 81.00 82.00 81.50 82225 83.00 83.75 84.25 85.75 86.75 85.00 88.25 87.50 88.00 89.75 90.25 92.00 91.25 93.75 92.75 94.25 95.50 96.25 97.50 97.00 99.25 Stock 35.00 25.50 26.25 25.75 26.25 27.00 26.75 27.75 28 25 28.00 28.75 28.75 29.75 30.50 30.75 32.25 33.00 33.75 32.75 34.00 34.50 35.00 34.75 34.00 36.75 Market Index 990.00 99438 998.64 1000.58 100234 1003.59 101737 103526 103638 1032.29 1046.17 1048.25 1053.25 1055.38 1049.89 1054.94 1060.53 1062.78 1068.73 1068.62 1072.75 1075.52 1078.75 1080.00 1084.25 Risk and Return Spreadsheet Example ASSIGNMENT NAME SAN LAR TIME Stock Clown 25.00 25.50 2625 25.75 263 Stock AN Closing Stock Closin A: Price Moth Price Ret De 1 5.00 Jan 12 67.00 formula 2.00 formula Feb 67.25 formula $1.50 formula March 67.75 formula 25 formula April 68.25 formula 83.00 formula May 67.50 forma 33.75 June 66.50 formula 34 35 formula July 67.75 formula 55.75 formule Aug 69.25 formula 86.75 formula Sept 68.75 formula 85.00 formula Oct. 70.35 forma 88.25 formula Now 71.00 formula 87.50 formula Dec 71.50 formula 88.00 formula Jan 13 70.25 formula 89.75 formula Feb 69.75 formula 90.25 formula March 71.50 formula 92.00 formula April 72.25 formula 91.25 formula 73.50 formula 93.75 formula 72.25 formula 92.75 formula July 73.75 formula 94.25 formula 74.50 formula 95.50 formula Sept. 76.25 formula 96.25 formula Oct. 78.00 formula 97.50 formula Nov. 77.00 formula 97.00 formula Dec 79,00 formula 99.25 formula 26.75 27.75 2825 28.00 28.75 28.75 29.75 30.50 30.75 32.25 33.00 33.75 32.75 34.00 34.50 35.00 34.75 34.00 36.75 Closing Mark's Reum Value R. 990.00 994 form 9964 for 1000 55 forma formula 100).59 for fon 1017.37 fon formula 1025 26 formula formula 101613 formula formula 1032.29 formula formula 1046.17 formula formula 1048.25 formula formula 1053.25 formula formala 1055.38 formula formula 1049 89 formula formula 1054.94 formula formula 1060.53 formula formula 1062.78 formula formula 1068.73 formula formula 1068 62 formala formula 1072.73 formula formula 1075.52 formula formula 1078.75 formula formula 1080.00 formula formula 1084.25 formula May June Aug Stock B Stock C Market Stock A Average Monthly Return formula Standard Deviation formula formula formula formula formula formula formula Beta Spreadsheet Example ASSIGNMENT NAME LAI TIME 1 Compute beta coefficients for all the stocks and report the repensionary output below Stock A Stock Stock 2. Calculation of Portfolio Beta and Portfolio Return Investmen Weighted Average Beta Average Weighted Monthly Average Return Return Stock Weight Beta Stock Weight Amount B formula formula formula 100% Portfolio Beta formula formula formala A formula formula B formula . formula formula formula 100% Portfolio Monthly Return formula Portfolio Annual Return formals formula formula 3. If the annual risk-free rute, Rit, will be 2 percent in 2014 and the expected retum on the market index, R., will be 8 percent, what is your portfolio's required rate of retum according to the CAPM? Ro-Ret+ (Ro-R:[]= formula Risk der Spreemple ASSIGNMENT LATINE C 65.00 35 1000 10035 101 27.15 foc 35 3335 2975 6725 BE March A 670 for 6650 67.75 for . 389 See 5 fo 35.00 Ot 7035 Now 71.00 formule 87.50 De 71.50 for Jam 70.35 for 89.75 Feb 69.75 forma March 71.50 for 92.00 April 72.35 for May 73.50 for 93.75 June 7325 formula 92.75 July 73.75 form 94.25 Aug 74.50 formula 95.50 Sept 76.25 formula Okt 78.00 formula 97:50 Nos. 77.00 formula 97.00 Dec 79.00 formula 99.25 female 10363 101239 117 104 fo 105325 fon for 105535 foc for 100 for 105454 53 fons 104.78 for fomu 106873 form form 1063 1072.75 for formula 1075 52 form formula 1078.75 for formal 100.00 forms form 105425 formula 33 00 33.95 1275 14.00 3450 35.00 34.75 3400 36.75 fo formula formos formula formula formula formula formula Stock B Stock Market Stock A Average Monthly Return formula Standard Deviation formula formula formula formala formula for for Beta Spreadsheet sample ASSONSENT NAME LASTING Cool and report the srock 2 Calculation of Portfolio Beta and Portfolio Return Weighted Average B Average Weighted Monthly Avenge Ratu Retu Imeste Stock Weight B Suck Weight About Sol B C for formula forma form B formule fone formal forma 100 Portfolio Monthly Return formula Portfolio Annual Return formula formula TOOS Portfolio Bet Formula formes 3. If the annual risk-free rate, Ret will be 2 percent in 2014 and the expected return on the market index, Rwill be 8 percent, what is your portfolio's required rate of return according to the CAPM? Ro-Re+ (Ro-Ro - formula 22 MODULE V: RISK AND RETURN INTRODUCTION To better understand the relationship between return and ris, we must know how return andre med tit. RATE OF RETURN If you buy at your pain or lose from that investment is called your return on investment. This return can be measured in two ways, in dollar tem or in percentage term. It is usually more convenient to summarize information about return in percentage term called rate of return. The rate of return is expressed as the change in value of an et plus any cash flows received during the period divided by the initial investment: R- P--P-P- PC P1 where R.- the actual rate of return during period, P-price (value) of asset at time - 1: P-price (value) of asset at time to cash flow roceived during the period from t-1 tot In the numerator of the above formula. Pe - Part is the capital gain or loss and is the dividend payment for a stock investment or interest payment for a bond investment. The first term on the right-hand side of the formula is called capital gains yield and the second term is called either dividend yield for a stock investment or current yield for a bond investment RISK The risk of concern to investors is the investment risk, which is related to the probability of low or negative returns. The greater the chance investors receive low returns, the riskier the investment. To quantify risk so that we can measure it, we generally deal with the probability distribution of rates of return. We can simply plot an investment's historical returns to construct a probability distribution. As the number of observations becomes large, say 60, the probability distribution will converge into a normal distribution, which has nice properties: (1) it is symmetrical around the mean; and (2) if you know both mean and standard deviation, you know all the distribution. Standard deviation is a statistical measure of the dispersion around the mean. The smaller the standard deviation, the tighter the probability distribution, and thus, the less risky the investment After computing rates of return for a time period, the mean and standard deviation of the eturn series can be calculated as follows: N ER- Mean (expected return) R - Standard Deviation N-1 Excel AVERAGE valuel, value2...) STDEV(value, value, ...) An asset's risk can be analyzed in two ways: (l) on a stand-alone basis, where the set is considered in isolation, and (2) in a portfolio context, where the set is included in a portfolio On a stand-alone basis. If an asset is not included in a portfolio, then standard deviation is its stand-alone risk, which is the risk that an investor would be exposed to Standard deviation measures the total risk of this asset. The smaller the standard deviation, the tighter the probability distribution, and accordingly, the lower the riskiness of the asset In a portfolio context. When an individual stock is held by itself, the risk measure is its standard deviation or total risk. Total risk, however, can be decomposed into two components: market risk and company specific risk. Market risk, or nondiversifiable risk, is the part of total risk that cannot be eliminated by diversification and stems from factors which systematically affoet most firms such as interest rate hikes, war, inflation, recessions, etc. On the other hand, company-specific risk, or diversifiable risk, is caused by such random events as lawsuits, strikes, and other events that are unique to a particular firm and it can be eliminated by proper diversification. Relevant risk. When investors are primarily concerned with portfolio risk rather than the risk of the individual securities in the portfolio, how should the riskiness of an individual stock be measured? One answer is provided by the Capital Asset Pricing Model (CAPM), which stipulates that there is a positive and linear relationship between a security's expected return and its systematic risk. In other words, the primary conclusion of the CAPM is that the relevant riskiness of an individual stock is its contribution to the riskiness of a well-diversified portfolio, or its market risk. Since market risk is the risk that remains after diversifying, it is inherent in the market and it can be measured by the degree to which a given stock tends to move or down with the market. CAPITAL ASSET PRICING MODEL (CAPM) ER)=R-f+IER)-RB where E(R) = the required rate of return on stock i; Ry the risk-free rate of return; E(R.) - the required rate of return on the market portfolio; and B - the beta coefficient of stock i. The beta of the market, Bu, is 1. 34 A mind why of a woman with the refund liebe couch which is of the Sovity wave that the stock bete officia de how the sockwffect the skiess of a diled portfolio, bestemor of 's risk Practically, the SAPS Index whose bisoul to one more them portfolio Irao be than 1 y 12, then this stock ve stock and is 30 per risker than the market wise, asock's be is less than 1. sy - then it is a defensivestock and is 40 perc less risky than the market To compute you must rely on historical return data. First, you need to collect past 60 monthly returns (five years of data of the stock and the overall market. Then, you regress the stock's returns against the market's returns in the following equation called the market model or the characteristie lines RE+BR where R stocki's return at time to the dependent variable of the regression R - market's retum at time to the independent variable of the regression - the constant term or the intercept of the regression: A -the beta coefficient of stock i or the slope of the regression; and the error term Using Excel to compute beta. Before using an analysis tool in Excel, you must arrange the data you want to analyze in columns of rows on your worksheet. This is your input range. The Data Analysis command is available in the Analysis group on the Data tab. If the Data Analysis command is not listed, you need to install the Analysis ToolPak in Microsoft Excel To install the Analysis ToolPak 1. Click File (on the top left corner) and then Option. Click Add-Ins and in the Add-Ins Inactive Application box, select the Analysis ToolPak check box, and then click GO next to the Manage box, and then click OK 3. After you load the Analysis ToolPak, the Data Analysis command is available in the Analysis group on the Data tab. SUMMARY OUTPUT Regression Statistics Multiple R 0.260823 0.068028 Adjusted R 0.025666 Square Standard Error 0.014815 R Square O ANOVA Regression Resid Total 01324 M 0.00015345057 0.000319 0.00035 0.00489 0.001 Upper repe X Variable 1 Car Se Lower 9 0.00359 0.00339967 0.0640 -0.00043 0.764330366 26723 0.21 0.29589 Lower 0309 -0.00042 -0.29589 Upper 95.0% 00136 1.2254 0.0136 1.2255 From the above output summary, the "Intercept" is a which equals 0.559% and the "X Variable is beta () which equals 0.76483. The beta of 0.76483 means that this stock is a defensive stock because its beta is less than the market beta of 1. When the market moves up (down) by 10 percent, this stock will move up (down) only 7.6483 percent PORTFOLIO RETURN AND BETA Once you compute ex post average returns and beta coeficients for all the stocks in the portfolio, you can compute the return on the portfolio, which is the weighted average of the individual stocks' returns, and the beta of the portfolio, which is the weighted average of the individual stocks" betas: N Rp = w;R,+W2R2+...+WnRN = w;R; and Bp = wiBi + W2B2+-+w.B- wiBi. where p = denotes portfolio; - the proportion of stock i relative to the portfolio's market value and the wi's must sum to 1; BA - the beta coefficient for stock i; and N w; = 1, which means that the sum of all proportions must equal 100 percent ZWI Risk and Return Exercisest Os January 2, 2014. you plan to invest $1.000.000 in three stocks to form a portfolio 5400.000 Stock A $200,000 in Stock Band 5400,000 in Stock C. To better se your portfoto's expected return and risk you decide to rely on the historical data of these three sing the past performance will be a good predictor for future performance. You have collected the monthly closing prices information for all three and the market index from December 2011 to December 2013 1. Create the spreadsheet and input the information given below. Next, calculate returns for each stock and the market index. All three stocks never pay dividends. Compute both mean and standard deviation of returns for all three stocks and the market index 2 Compute beta coefficients for all three stocks and report their respective regression ummary output. Next, calculate your portfolio's annual return and beta If the risk-free rate, nar, and the expected return on the market index, i, for 2014 will be 2 percent and 8 percent, respectively, what is your portfolio's required rate of return according to the CAPM? Month Dec. 2011 Jan 2013 Feb March April Mary June July Awe Sept Oct. Nov. Dec Jan. 2013 Feh March April May June July Aug Sept Oct Nov. Des Stock 65.00 67.00 67.25 67.75 68.25 67.50 66.50 67.75 69.25 68.75 70.25 71.00 71.50 70.25 69.75 71.50 72.25 73.50 72.25 73.75 74.50 76.25 78,00 77.00 79.00 Stock B 81.00 82.00 81.50 82225 83.00 83.75 84.25 85.75 86.75 85.00 88.25 87.50 88.00 89.75 90.25 92.00 91.25 93.75 92.75 94.25 95.50 96.25 97.50 97.00 99.25 Stock 35.00 25.50 26.25 25.75 26.25 27.00 26.75 27.75 28 25 28.00 28.75 28.75 29.75 30.50 30.75 32.25 33.00 33.75 32.75 34.00 34.50 35.00 34.75 34.00 36.75 Market Index 990.00 99438 998.64 1000.58 100234 1003.59 101737 103526 103638 1032.29 1046.17 1048.25 1053.25 1055.38 1049.89 1054.94 1060.53 1062.78 1068.73 1068.62 1072.75 1075.52 1078.75 1080.00 1084.25 Risk and Return Spreadsheet Example ASSIGNMENT NAME SAN LAR TIME Stock Clown 25.00 25.50 2625 25.75 263 Stock AN Closing Stock Closin A: Price Moth Price Ret De 1 5.00 Jan 12 67.00 formula 2.00 formula Feb 67.25 formula $1.50 formula March 67.75 formula 25 formula April 68.25 formula 83.00 formula May 67.50 forma 33.75 June 66.50 formula 34 35 formula July 67.75 formula 55.75 formule Aug 69.25 formula 86.75 formula Sept 68.75 formula 85.00 formula Oct. 70.35 forma 88.25 formula Now 71.00 formula 87.50 formula Dec 71.50 formula 88.00 formula Jan 13 70.25 formula 89.75 formula Feb 69.75 formula 90.25 formula March 71.50 formula 92.00 formula April 72.25 formula 91.25 formula 73.50 formula 93.75 formula 72.25 formula 92.75 formula July 73.75 formula 94.25 formula 74.50 formula 95.50 formula Sept. 76.25 formula 96.25 formula Oct. 78.00 formula 97.50 formula Nov. 77.00 formula 97.00 formula Dec 79,00 formula 99.25 formula 26.75 27.75 2825 28.00 28.75 28.75 29.75 30.50 30.75 32.25 33.00 33.75 32.75 34.00 34.50 35.00 34.75 34.00 36.75 Closing Mark's Reum Value R. 990.00 994 form 9964 for 1000 55 forma formula 100).59 for fon 1017.37 fon formula 1025 26 formula formula 101613 formula formula 1032.29 formula formula 1046.17 formula formula 1048.25 formula formula 1053.25 formula formala 1055.38 formula formula 1049 89 formula formula 1054.94 formula formula 1060.53 formula formula 1062.78 formula formula 1068.73 formula formula 1068 62 formala formula 1072.73 formula formula 1075.52 formula formula 1078.75 formula formula 1080.00 formula formula 1084.25 formula May June Aug Stock B Stock C Market Stock A Average Monthly Return formula Standard Deviation formula formula formula formula formula formula formula Beta Spreadsheet Example ASSIGNMENT NAME LAI TIME 1 Compute beta coefficients for all the stocks and report the repensionary output below Stock A Stock Stock 2. Calculation of Portfolio Beta and Portfolio Return Investmen Weighted Average Beta Average Weighted Monthly Average Return Return Stock Weight Beta Stock Weight Amount B formula formula formula 100% Portfolio Beta formula formula formala A formula formula B formula . formula formula formula 100% Portfolio Monthly Return formula Portfolio Annual Return formals formula formula 3. If the annual risk-free rute, Rit, will be 2 percent in 2014 and the expected retum on the market index, R., will be 8 percent, what is your portfolio's required rate of retum according to the CAPM? Ro-Ret+ (Ro-R:[]= formula Risk der Spreemple ASSIGNMENT LATINE C 65.00 35 1000 10035 101 27.15 foc 35 3335 2975 6725 BE March A 670 for 6650 67.75 for . 389 See 5 fo 35.00 Ot 7035 Now 71.00 formule 87.50 De 71.50 for Jam 70.35 for 89.75 Feb 69.75 forma March 71.50 for 92.00 April 72.35 for May 73.50 for 93.75 June 7325 formula 92.75 July 73.75 form 94.25 Aug 74.50 formula 95.50 Sept 76.25 formula Okt 78.00 formula 97:50 Nos. 77.00 formula 97.00 Dec 79.00 formula 99.25 female 10363 101239 117 104 fo 105325 fon for 105535 foc for 100 for 105454 53 fons 104.78 for fomu 106873 form form 1063 1072.75 for formula 1075 52 form formula 1078.75 for formal 100.00 forms form 105425 formula 33 00 33.95 1275 14.00 3450 35.00 34.75 3400 36.75 fo formula formos formula formula formula formula formula Stock B Stock Market Stock A Average Monthly Return formula Standard Deviation formula formula formula formala formula for for Beta Spreadsheet sample ASSONSENT NAME LASTING Cool and report the srock 2 Calculation of Portfolio Beta and Portfolio Return Weighted Average B Average Weighted Monthly Avenge Ratu Retu Imeste Stock Weight B Suck Weight About Sol B C for formula forma form B formule fone formal forma 100 Portfolio Monthly Return formula Portfolio Annual Return formula formula TOOS Portfolio Bet Formula formes 3. If the annual risk-free rate, Ret will be 2 percent in 2014 and the expected return on the market index, Rwill be 8 percent, what is your portfolio's required rate of return according to the CAPM? Ro-Re+ (Ro-Ro - formula