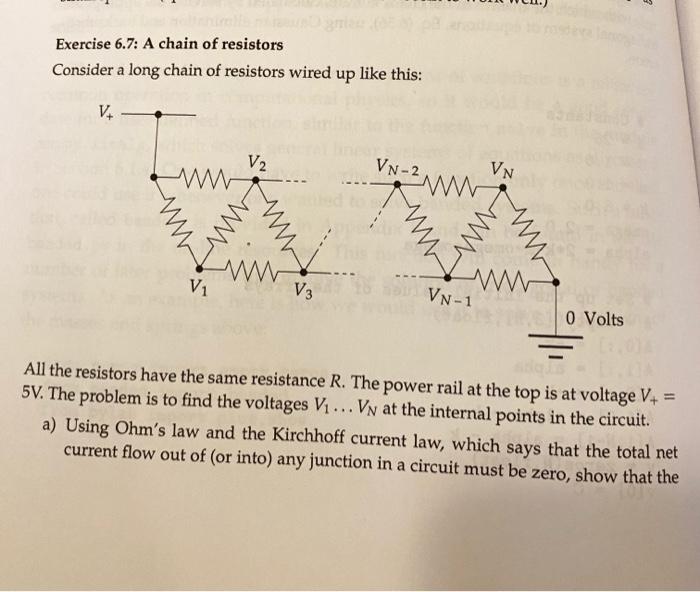
I need to solve this problem with Python using Colab! Please don't give me a hand writen solution! I need the code! I always reward with an upvete if I get what I requested. 45 Exercise 6.7: A chain of resistors Consider a long chain of resistors wired up like this: V2 VN+2 WWW VN ww ww ww ww En WW WW w www V1 ww VN-1 V3 0 Volts All the resistors have the same resistance R. The power rail at the top is at voltage V+ = 5V. The problem is to find the voltages V... Vy at the internal points in the circuit. a) Using Ohm's law and the Kirchhoff current law, which says that the total net current flow out of (or into) any junction in a circuit must be zero, show that the 6.2 | EIGENVALUES AND EIGENVEC voltages Vi... Vy satisfy the equations 3V - V2 - V3 = V+ - V1 +4V2 - V3 - V4 = V+, : -V-2-V-1 +4V; - Vi+1 - Vi+2 = 0, : -VN-3 - VN-2+4VN-1 - VN = 0, -VN-2 - VN-1 +3Vp = 0. Express these equations in vector form Av = w and find the values of the ma- trix A and the vector w. b) Write a program to solve for the values of the Vi when there are N = 6 internal junctions with unknown voltages. (Hint: All the values of V should lie between zero and 5V. If they don't something is wrong.) c) Now repeat your calculation for the case where there are N = 10 000 internal junctions. This part is not possible using standard tools like the solve function. You need to make use of the fact that the matrix A is banded and use the banded function from the file banded.py, discussed in Appendix E. E.2 | SOLUTION OF TRIDIAGONAL OR BANDED SYSTEMS OF EQUATIC matrix was like this: doo doi 402 410 411 412 413 A= 221 222 223 224 (E.2) 432 433 434 14344/ That is, it has two nonzero elements above the diagonal, one below, and four nonzero diagonals in all. We would represent this with a four-row array A having elements as follows: ROZ 424 do: 012 423 49 (E.3) doo 211 822 23 24 10 421 432 43- The values in the elements marked "-" do not matter-you can put anything in these elements and it will make no difference to the results. The vector v is stored in the array v in standard form-no special arrangement is used. The function banded returns a single array with the same length as v con- taining the solution x to the equations, or, in the case of multiple right-hand sides, an array with the same shape as v with the solution for each of the right- hand sides in the corresponding column. from numpy import copy File: banded.py det banded (Aa,va, up, down): A= copy (Aa) v = copy(va) N = len() # Gaussian elimination for in range (N): # Normalization factor div - A Cup,m) # Update the vector first v[a] /= div for k in range(1, down+1): 1 +k<:>