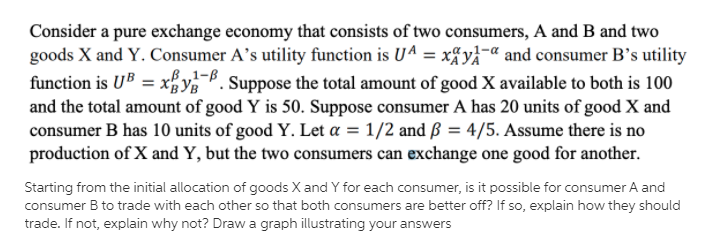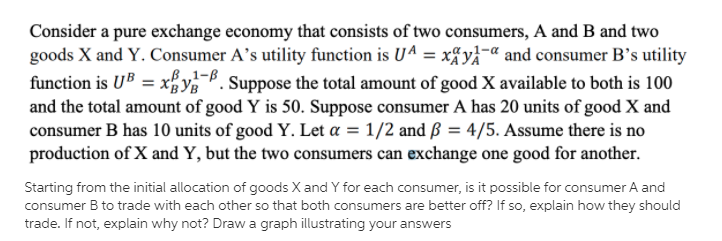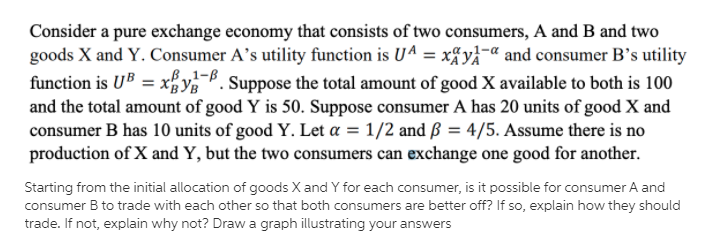


,. I need your input here
General equilibrium and externalities/public goods [25 points] [Note that parts (a) - (b) are separate from parts (c) - (e).] Consider a two-good/two-person pure-exchange economy. The respective utility functions for each individual consumer (agent) are given by U() = x+ 3y , U(2) = xty . where x and y denote quantities of consumption goods. The first agent holds an initial allocation of w(): (x = 6; y = 5} and the second an initial allocation of w(2): {x = 7;y = 4). Assume that the agents can exchange x and y with one another. (a) Draw the Edgeworth box for this economy clearly indicating where the initial allocation lies and what the sides of the box measure. Then, indicate the set of points in the Edgeworth box that are a Pareto improvement with respect to the endowment point. (b) In another Edgeworth box, indicate the possible Pareto optimal allocations of x and y after trade has taken place. Explain the intuition for your solution. Now consider externalities. (c) Suppose that the (inverse) market demand curve for good X is given by P(X) = X-2, X > 0. The marginal social cost of producing it is MSC(X) = 8X, whereas the marginal private cost of producing good X is MPC(X) = X. Based on this information, and assuming that X is produced in an (unregulated) competitive market, carefully explain why the quantity of the commodity produced would not be socially efficient. Then, provide a "real world" example of a commodity that good X might represent and its implications for third-party consumers or producers.Consider a pine exchange economyr that consists of two consumers, A and B and two goods X and Y. Consumer A's utilityF mction is U A = xfyj'\" and consumer B's utility fimction is ll}r = xgyg-B. Suppose the total amount of good X available to both is 10!] and the total amount of good '1' is 50. Suppose consumer A has 26 units of good X and consumerB has 10 units ofgoodY. Let cr = 13'2 and!)I = 4.5. Assume there is no production of X and Y, but the two consumers can exchange one good for another. Starting from the initial altocation of goods X and '1' for each consumer, is it possible for consumer A and consumer B to trade with each other so that both consumers are better off? If so, explain how they should trade. if not, explain why:r not? Draw a graph illustrating your answers Consider a twoperiod model of a small open economy with a single good each period. Let preferences of the representative household be described by the utility function lnl[C1} + ln[C2}, where C1 and C2 denote consumption in periods 1 and 2, respectively, and In denotes the natural logarithm. |n period 1, the household receives an endowment of [31 = 1D. In period 2, the household receives prots, denoted by [Pie sign]I2, from the firms it owns. Households and firms have access to financial markets where they can borrow or lend at the interest rate r1. {r1 is the interest rate on assets held between periods 1 and 2.} Firms invest in period 1 to be able to produce goods in period 2. The production technology in period 2 is given by G2 = squareroot of IL where 02 and Il denote, respectively, output in period 2 and investment in period 1. Assume that there exists free international capital mobility and that the world interest rate, r" = 10% per period .e., r* = [1.1]. Finally, assume that the economy's initial net foreign asset position is zero [B_D"'* = {l}. Compute the nn's optimal levels of period1 investment and period2 profits. State the maximization problem of the representative household and solve for the optimal levels of consumption in periods 1 and 2 Find the country-\"s net foreign asset position at the end of period 1, the trade balance in periods 1 and 2, and the current account in periods 1 and 2. Now consider an investment surge. Specically, assume that as a result of a technological improvement, the production technology becomes D2 = 21l[|_1 ]. Find the equilibrium levels of saving, investment, the trade balance, the current account, and the courrtrfs net foreign asset position in period 1. Compare your results with those obtained in items [al [cl providing interpretation and intuition. where (3'1 and 0: denote consumption in periods 1 and 2. In both periods, the household receives prots from the rm it owns. denoted H1 and H2. Households and rms have access to nancial markets 1Where the};r can borrow or lend at the interest rate n. The production technologiesinperiodsl and2aregivenhy Q1 = A1]? and Q: = A21? where Q1 and Qg denote output in periods 1 and 2, In and I1 denote the capital stool: in periods 1 and 2. A] and A2 denote the productivity factors in periods 1 and 2. and o is a parameter. Assume that ID = 113, A1: 3%. A: = 3.2, and c: = 3. At the beginning oi'period 1 households have 3!; = 3 bonds. The interest rate on bonds held eem peried e to period 1 is re = 0.25. In period 1, rms borrow the amount Dir to purchase investment goods that become productive capital in period 2, I]. Amume that there exists free international capital mobility and that the 1world intermt rate1 denoted r", is 20 percent. 3. Compute output and prots in period 1. b. Compute the optimal levels of investment in perimi 1 and output and prots in period 2. c. Solve for the optimal levels of oonsumption in periods 1 and 2. d. Find the country's net foreign asset position at the end of period 1, denoted Bf. saving. 31, trade halanoe, T31, and current acoount. CA1