I really need help with these practice questions pleasee .

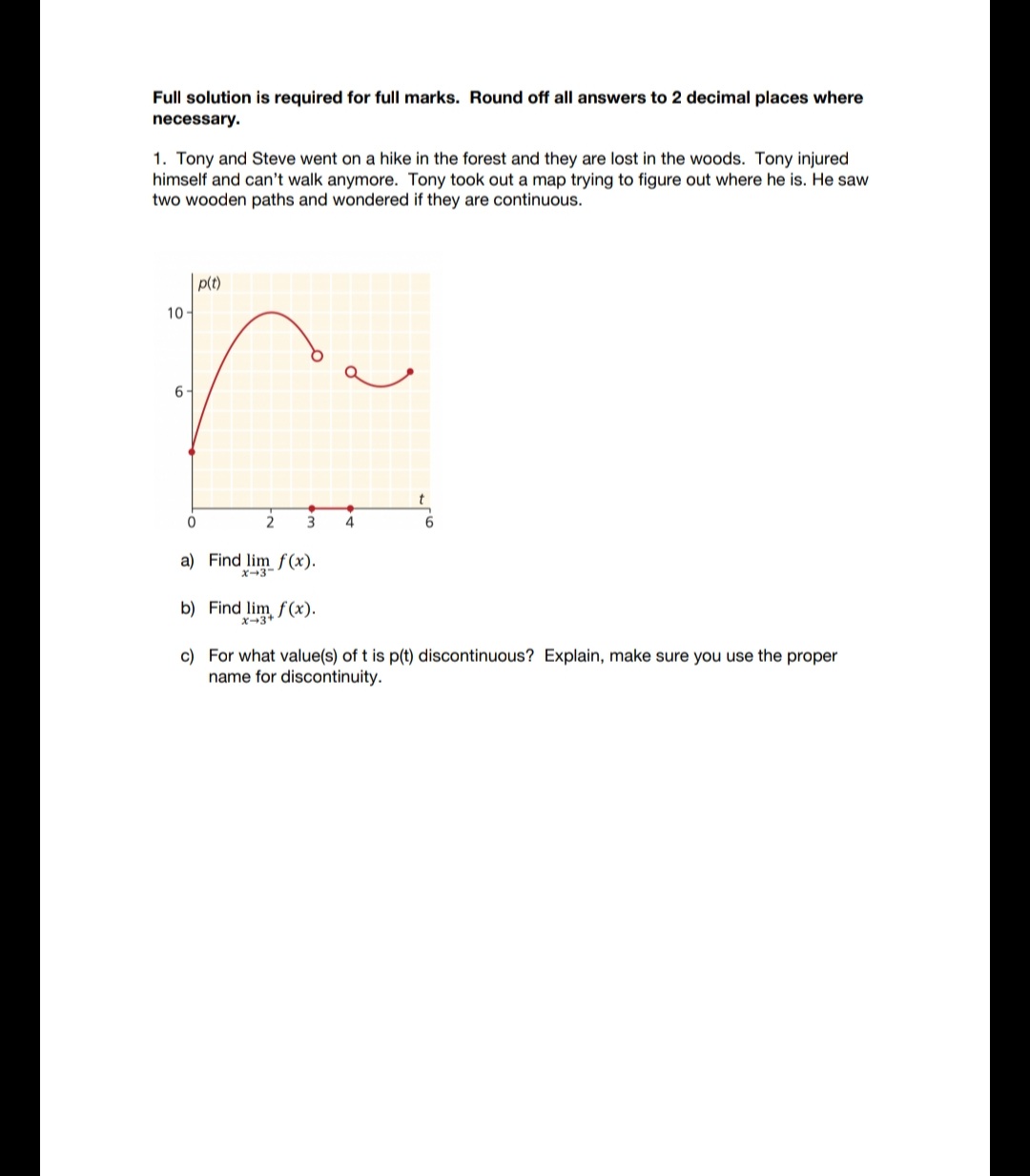
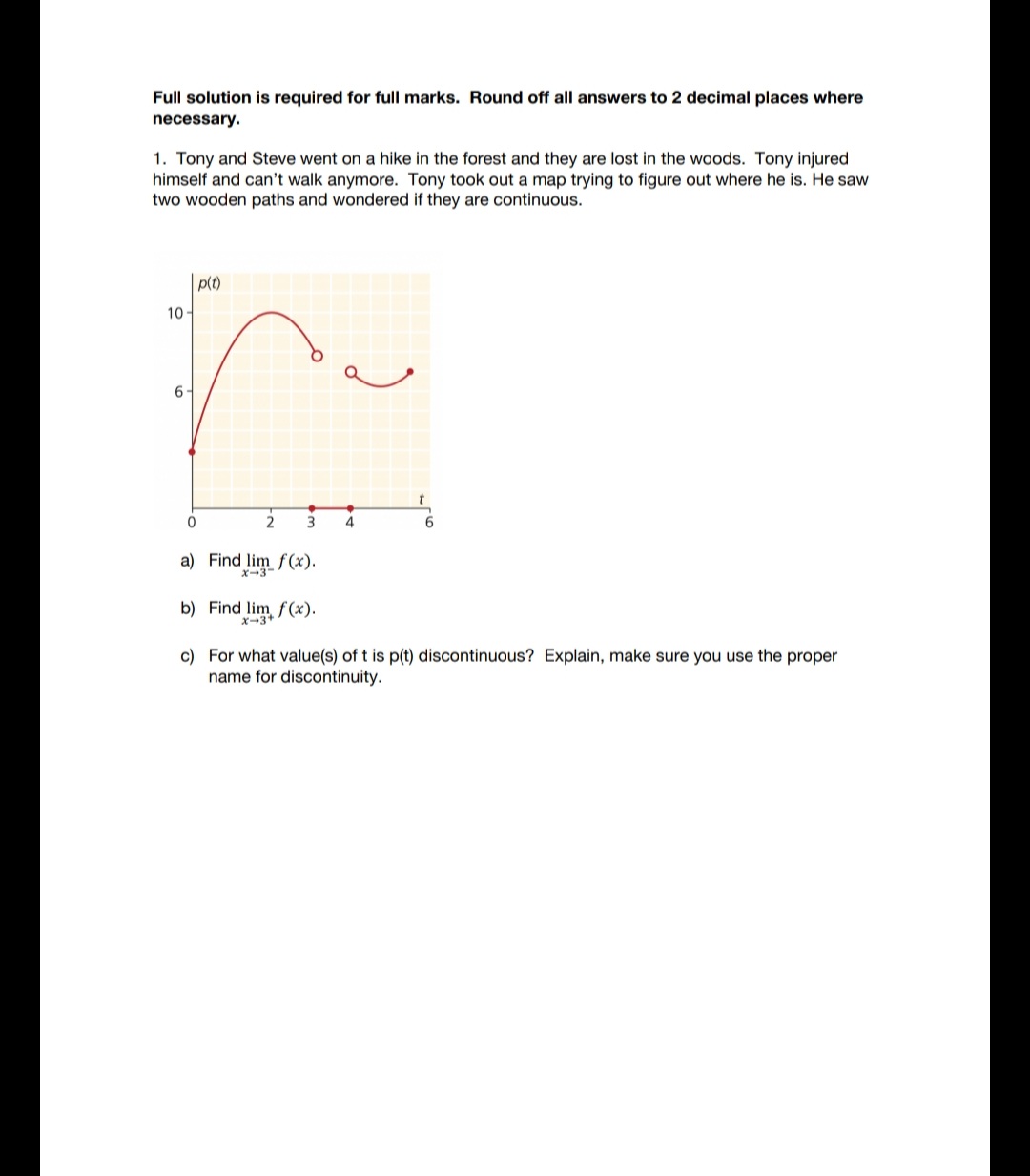
Full solution is required for full marks. Flound off all answers to 2 decimal places where necessary. 1. Tony and Steve went on a hike In the forest and they are lost In the woods. Tony Injured himself and can't walk anymore. Tony took out a map trying to figure out where he Is. He saw two wooden paths and wondered If they are continuous. pit) to- 6- O\\_/ r.eot. 0 2 3 4 6 a) Find lim f(x). x-US' in) Find 1\"}; for). c) For what valueis] of t ls p{t) discontinuous? Explain. make sure you use the proper name for discontinuity. 2. Steve leaves Tony at Point P. Steve walks 4 km on a bearing of 040. then a further 6 km on a bearing of 155 to reach to the camp site to get some medical supplies. To save time. he hikes directly back to point P from the camp site. a) Draw a diagram to illustrate the situation. b) What is the direct distance from Point P to the camp site? c) On what bearing should Steve walk back from the camp site to return to point P. 3. As it gets darker outside. Steve is lost in the woods. and he calls for help. A helicopter at Point A (6. 9. 3) moves with constant velocity in a straight line. 10 minutes later it is at Point B (3. 10. 2.5). Distances are in kilometres. a) Find Vector AB. b) Find the helicopter's speed. in kmfhour. c) Determine the vector equation of the straight line path of the helicopter. d) Steve is at point U (7. 2. 4}. determine the shortest distance from point U to the path of the helicopter 4. Two other helicopters are also coming for the rescue. Helicopter K's position after t seconds is given by: x(t) = 5 - 2t. y[t) = 4 - 3t. z(t) = 4 + 4t Helicopter M's position aftert seconds is given by: x(t) = 1. y(t} = - 4 - 2t. 2(t] = 14 + 21 All distance units are in metres. E.) Find the initial position of each helicopter. b) Find the velocity vector of each helicopter. c) Will the helicopters collide? Explain why or why not. 5. After Tony and Steve got off the helicopter. they were picked up by an ambulance. The I ambulance moves In a straight line with position given by s{t) = Bae' 40t m where t is time in seconds. t 2 0. a) Find the velocity and acceleration functions. b) Find the initial position. velocity. and acceleration of the ambulance. c) Find the exact time when the velocity Is 44 ms"