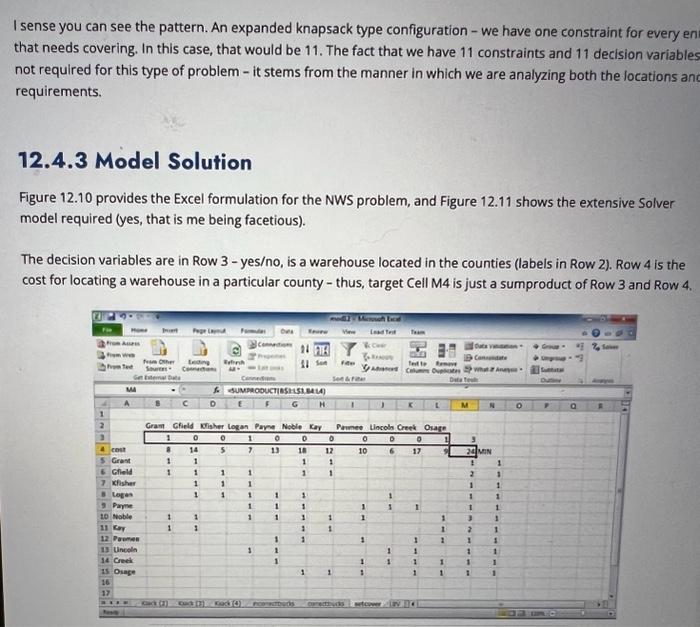
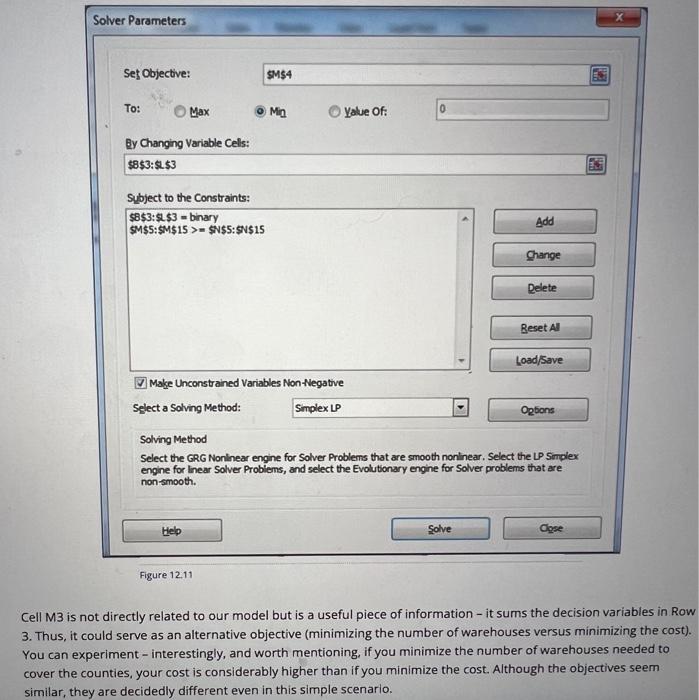
I sense you can see the pattern. An expanded knapsack type configuration - we have one constraint for every en that needs covering. In this case, that would be 11. The fact that we have 11 constraints and 11 decision variables not required for this type of problem - it stems from the manner in which we are analyzing both the locations ant requirements. 12.4.3 Model Solution Figure 12.10 provides the Excel formulation for the NWS problem, and Figure 12.11 shows the extensive Solver model required (yes, that is me being facetious). The decision variables are in Row 3 - yeso, is a warehouse located in the counties (labels in Row 2). Row 4 is the cost for locating a warehouse in a particular county - thus, target Cell M4 is just a sumproduct of Row 3 and Row 4. 12.4.1 Problem Description: NWS Problem The NWS has commissioned the creation of a number of storage warehouses in North Central Oklahoma to store research equipment that trained weather spotters can use to assist in severe weather research. Such equipment includes mobile radars, specific weather balloon technology, Helen Hunt's phone number, etc. The 11-county region is shown below. It does not include Canadian, Oklahoma, Okfuskee counties. There has been some work done in identifying potential locations within each county. One combined value has been calculated that represents a measure of cost/accessibility for each county. Small is better. This information is shown below. Find the least-cost way to locate NWS storage warehouses that covers all counties; each of the 11 counties should have a warehouse either in it or in a contiguous county. (1) Make Unconstrained Variables Non-Negative Select a Solving Method: Solving Method Select the GRG Nonlinear engine for Solver Problems that are smooth noninear. Select the LP Sirplex engine for Inear Solver Probiems, and select the Evolutionary engine for Solver problems that are non-smooth. Figure 12.11 Cell M3 is not directly related to our model but is a useful piece of information - it sums the decision variables in Row 3. Thus, it could serve as an alternative objective (minimizing the number of warehouses versus minimizing the cost). You can experiment - interestingly, and worth mentioning, if you minimize the number of warehouses needed to cover the counties, your cost is considerably higher than if you minimize the cost. Although the objectives seem similar, they are decidedly different even in this simple scenario. (1) Make Unconstrained Variables Non-Negative Select a Solving Method: Solving Method Select the GRG Nonlinear engine for Solver Problems that are smooth noninear. Select the LP Sirplex engine for Inear Solver Probiems, and select the Evolutionary engine for Solver problems that are non-smooth. Figure 12.11 Cell M3 is not directly related to our model but is a useful piece of information - it sums the decision variables in Row 3. Thus, it could serve as an alternative objective (minimizing the number of warehouses versus minimizing the cost). You can experiment - interestingly, and worth mentioning, if you minimize the number of warehouses needed to cover the counties, your cost is considerably higher than if you minimize the cost. Although the objectives seem similar, they are decidedly different even in this simple scenario. Assume that the four square counties in the northwest corner are all contiguous to each other. Also, assume thi Creek and Osage counties are contiguous. All other relationships should be visually obvious, It is permissible to I overlap, meaning multiple warehouses can be next to a particular county. Note: Further geospatial research has shown that Creek and Osage county are NOT contiguous (by a matter of fo seems). No matter, we will continue to assume they are. Cartographers, I apologize for this inaccuracy. 12.4.2 Modeling Preliminaries As mentioned earlier, this is a classic "set covering" model (don't you just love all the terminology?). One wishes to find the optimal set of warehouse locations that cover all counties. A lot of cell phone tower design algorithms use this basic concept, and you can probably think of other application areas as well. The decisions to be made: In which of the 11 counties should we place warehouses? Thus, this equates to eleven of decision variables, indicating yes or no, as to whether a warehouse should be located in a certain county. The objective is to minimize cost - that is a basic formula with 11 terms using the provided cost information. The covering constraints for these types of problems are the key component. Much like the scheduling models seen previously, in which we wanted to staff shifts such that our hourly requirements were AT LEAST met, here, we want to locate warehouses such that every county has AT LEAST one warehouse either in it or next to it. It is typically not reasonable to expect that we could EXACTLY have one warehouse cover every county (likely infeasible), although minimizing the overlap (where we exceed the minimum required number) might be a secondary objective (or a primary one for that matter). Of course, in the case of cell phone design or even in this hypothetical scenario, we might want design redundancy! To create these constraints, let us examine Grant County. Grant County is covered if a warehouse is located in Grant County (no kidding!) or in the three other counties that are contiguous - Kay, Noble, or Garfield. Mathematically then, this constraint for Grant County is: GRANT + KAY + NOBLE + GARFIELD > = 1 Similarly, then, for GARFIELD county: GARFIELD + GRANT + KAY + NOBLE + LOGAN + KINGFISHER >=1. Rows 5 through 15 are the constraints for each county. The " 1 " indicates that the county represented by that column (decision variable indicator for a warehouse) covers that county - a blank implies it does not. Column M is again our action column - it is a sumproduct of Row 3 multiplied by the corresponding row of interest. The formula one would input in Cell M5, to be copied down the column : =SUMPRODUCT(B\$3:L\$3, B5:L5). The coverage constraints are simply Column M>= Column N. The solution to the model shows that the least cost way of locating warehouses is to place them in Grant, Logan and Osage County, for a cost of 24 units. All counties are covered by this warehouse arrangement, and three counties are covered by more than one warehouse location (Garfield, Noble and Kay counties). As an aside, there is a solution to this situation in which you can have EXACTLY one warehouse cover each county. That is a rarity in this type of problem, and if I could change the county configuration of Oklahoma to make this go away so that a student wouldn't accidently get the wrong idea, I would. But the governor turned down my reconfiguration of boundary request. So I mention the anomaly here. There is one more modeling scenario that l'd like to present that uses binary variables in a unique way - what I call "linking" variables or problems with linking aspects. In this case, by the use of the binary variables, we link different decisions together in one model that allows us to have a more global view of a situation that will lead to a more comprehensive and reasonable suggested solution