I solved Question 8.11. Please show me the detailed work and steps for Question 8.12.

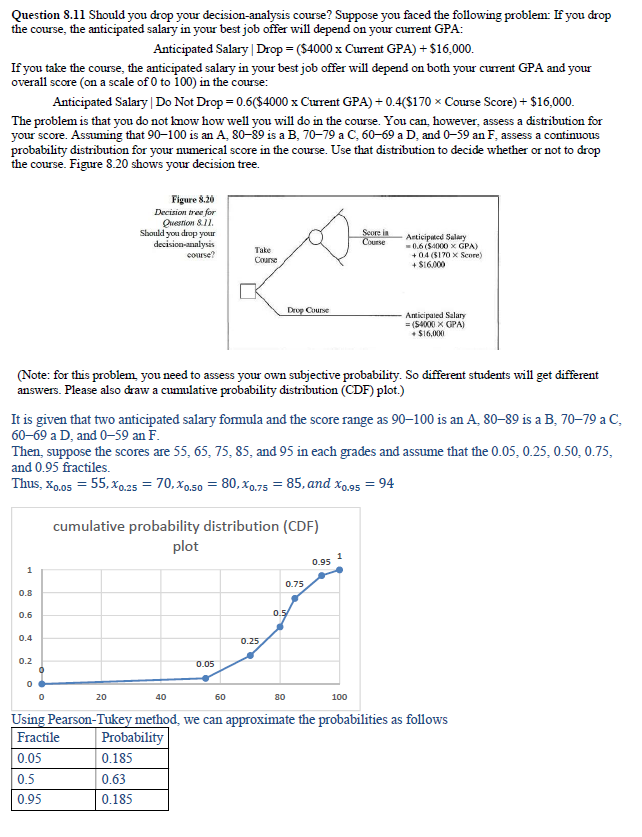
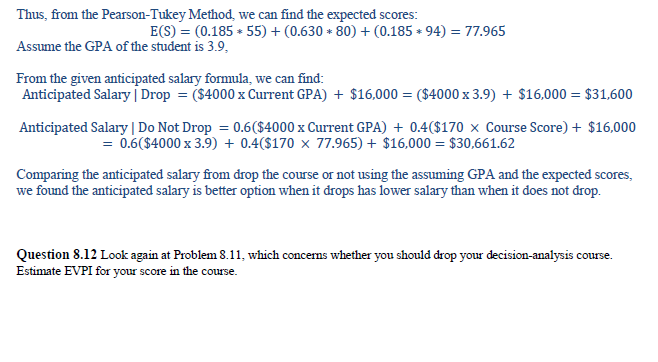
Question 8.11 Should you drop your decision-analysis course? Suppose you faced the following problem: If you drop the course, the anticipated salary in your best job offer will depend on your current GPA: Anticipated Salary | Drop = ($4000 x Current GPA) + $16,000. If you take the course, the anticipated salary in your best job offer will depend on both your current GPA and your overall score (on a scale of 0 to 100) in the course: Anticipated Salary | Do Not Drop = 0.6($4000 x Current GPA) + 0.4($170 * Course Score) + $16,000. The problem is that you do not know how well you will do in the course. You can, however, assess a distribution for your score. Assuming that 90-100 is an A, 80-89 is a B, 70-79 a C, 60-69 a D, and 0-59 an F, assess a continuous probability distribution for your numerical score in the course. Use that distribution to decide whether or not to drop the course. Figure 8.20 shows your decision tree. Figure 8.20 Decision tree for Question 8 11. Should you drop your Score in decision-analysis Course Articipated Salary -0.6 (540 X GPA) course? Take Course + 04 ($170 X Score) + $16.000 Drop Course Anticipated Salary (54000 X GPA) * $16,000 (Note: for this problem, you need to assess your own subjective probability. So different students will get different answers. Please also draw a cumulative probability distribution (CDF) plot.) It is given that two anticipated salary formula and the score range as 90-100 is an A, 80-89 is a B. 70-79 a C, 60-69 a D, and 0-59 an F. Then, suppose the scores are 55, 65, 75, 85, and 95 in each grades and assume that the 0.05, 0.25, 0.50, 0.75, and 0.95 fractiles. Thus, Xo.05 = 55, X0.25 = 70, X0.50 = 80,x0.75 = 85, and *0.95 = 94 cumulative probability distribution (CDF) plot 0.95 1 0.75 0.6 0.4 0.25 0.2 0105 20 40 60 80 100 Using Pearson-Tukey method, we can approximate the probabilities as follows Fractile Probability 0.05 0.185 0.5 0.63 0.95 0.185Thus, from the Pearson-Tukey Method, we can find the expected scores: E(S) = (0.185 * 55) + (0.630 * 80) + (0.185 * 94) = 77.965 Assume the GPA of the student is 3.9, From the given anticipated salary formula, we can find: Anticipated Salary | Drop = ($4000 x Current GPA) + $16,000 = ($4000 x 3.9) + $16,000 = $31,600 Anticipated Salary | Do Not Drop = 0.6($4000 x Current GPA) + 0.4($170 x Course Score) + $16,000 = 0.6($4000 x 3.9) + 0.4($170 x 77.965) + $16,000 = $30,661.62 Comparing the anticipated salary from drop the course or not using the assuming GPA and the expected scores, we found the anticipated salary is better option when it drops has lower salary than when it does not drop. Question 8.12 Look again at Problem 8.11, which concerns whether you should drop your decision-analysis course. Estimate EVPI for your score in the course