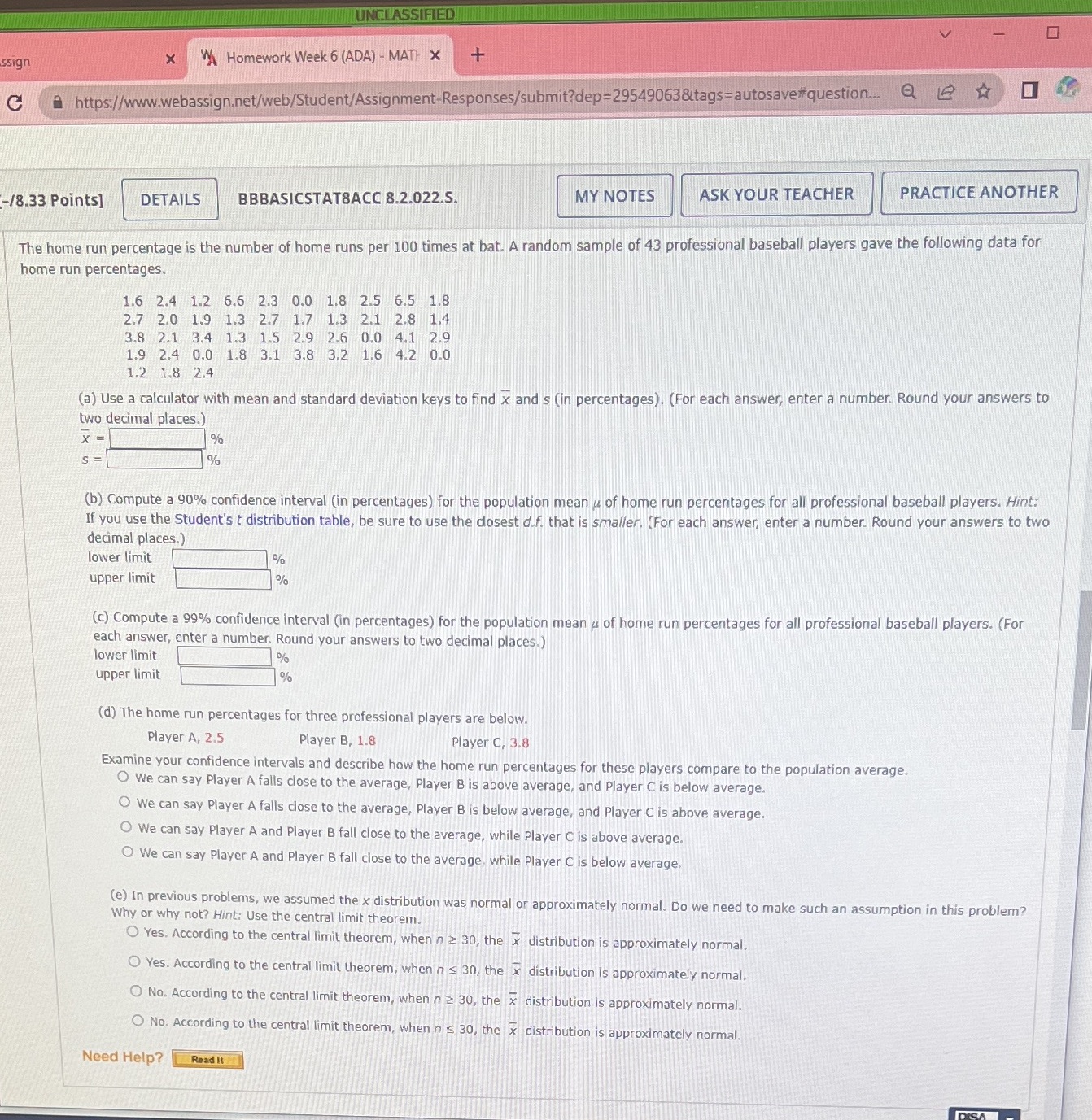
I The home run percentage is the number of home runs per 100 times at bat. A. ran home run percentages. 1.6 2.4 1.2 6.6 2.3 0.0 1.3 2.5 6.5 1.3 . . . . .. 2.7 2.o 1.9 1.3 2.7 1.7 1.3 2.1 2.8 1.4 _ -_ .. ._ _- _ 3.8 2.1 3.4 1.3 1.5 2.9 2.6 0.0 4.1 2.9 . . .- . . I-._ - - _ 1.9 2.4 0.0 1.8 3.1 3.8 3.2 1.6 4,2 0.0 1.2 1.8 2.4 H ' ' ' wens to (a) Use a calculator with mean and standard deviation keys to nd it and s (in percentages}. (For each answer, enter a number. Round your ans two decimal places.) 32 = or. s = \"it (b) Compute a 90% condence interval (in percentages}. for the population mean ,u of home run nercentagesfor all professional baseball plBYeTS- HIM- lf you use the Student's t distribution table, be sure to use the closest of. that is smallen i For each answer. enter a number. Round your answers to two decimal places.) lower limit % upper limit "it: (c) Compute a 99% condence interval (in percentages) for the population mean it of home run percentages for all professional baseball players. {For each answer. enter a number. Round your answers to two decimal places.) lower limit % upper limit 9i: (:1) The home run percentages for three professional players are below. Player A, 2.5 Player B, 1.3 Player C, 3.8 Examine your condence intervals and describe how the hp 0 We can say Player A falls dose to the average, me run percentages for these players compare to the population average. Player 3 is above average. and Player C is below average. 0 We can say Player A fails dose to the average, Player B is below average, and Player -C is above average. 0 We can say Player A and Player B fall close to the average, while Player C is above average. 0 We ran say PlayerA and Player Bfall close to the average, while Player C is below average. (e)1n previous problems, we assumed the 1: distribution was normal Why or why not? Hint: Use the central limit theorem. 0 Yes. According to the central limit theorem, when n 2 30, or approximately normal. Do we need to make such an assumption in this problem? i the ; distribution is approximately normal. ' 0 Yes. According to the central limit theorem, when n s .30. the E distribution is approximately normal. 0 No. According to the central limit theorem. when n\" 2 39, the E\" distribution ls approximately normal. 0 No. According to the central limit theorem, when n5 30' rue I distribution Is approximately nonnal