I tried following the steps exactly but I am still getting the answers wrong. Can you use the outline to answer this problem in more understandable terms?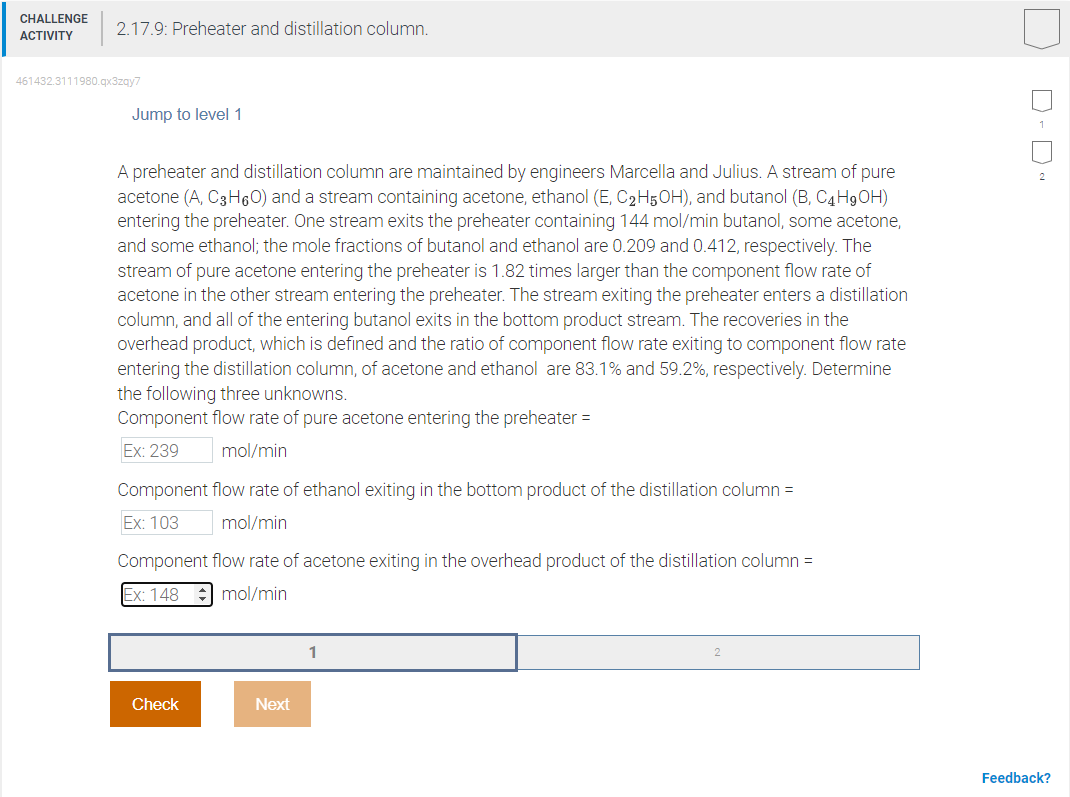

A preheater and distillation column are maintained by engineers Marcella and Julius. A stream of pure acetone (A,C3H6O) and a stream containing acetone, ethanol (E,C2H5OH), and butanol (B1C4H9OH) entering the preheater. One stream exits the preheater containing 144mol/min butanol, some acetone, and some ethanol; the mole fractions of butanol and ethanol are 0.209 and 0.412, respectively. The stream of pure acetone entering the preheater is 1.82 times larger than the component flow rate of acetone in the other stream entering the preheater. The stream exiting the preheater enters a distillation column, and all of the entering butanol exits in the bottom product stream. The recoveries in the overhead product, which is defined and the ratio of component flow rate exiting to component flow rate entering the distillation column, of acetone and ethanol are 83.1% and 59.2%, respectively. Determine the following three unknowns. Component flow rate of pure acetone entering the preheater = mol/min Component flow rate of ethanol exiting in the bottom product of the distillation column = mol/min Component flow rate of acetone exiting in the overhead product of the distillation column = mol/min Step 2. The basis flow rate is the butanol component flow rates in Stream 2: n2,B=204minmol Step 3. Each unit represents a system. The preheater subsystem is selected first. Steps 4, 5, and 6. Mole balances are logical, since no reactions occur. n1,A+n2,A=n3t,An2,E=n3,En2,B=n3,B Step 7. Extra equations include a ratio of flow rates for acetone, sums of the mole fractions in Stream 2, and component to total flow rate relationship. n1,A=1.82n2,Ax3,Bn3=n3,Bx2,A+x2,E+x2,B=1x3,A+x3,E+x3,B=1 Step 8. Seven unknowns are: n1,n2,x2,A,x2,E,x2,B,n3,x3,A Step 9. Seven unknowns match seven equations. Therefore, the system will be solved before moving on to the next subsystem (Step 10). Step 11. The B extra equation finds the total flow rate of Stream 3. n3=x3,Bn3,B=0.209204minmol=976minmol Next, the mole fraction of A in Stream 3 is found. x3,A+x3,E+x3,B=x3,A+0.412+0.209=1x3,A=0.379 Combining the mole balance and extra equation for A finds the other two A flow rates. 1.82n2,A+n2,A=n3,An2,A=131minmoln1,A=n3,An2,An1,A= The E flow rates is found from the mass balance. n3,E=0.412976minmol=402minmol Step 3. The distillation column is the next system of interest. Steps 4, 5, and 6. Mole balances are appropriate here also. n3,A=n4,A+n5,An3,E=n4,E+n5,En3,B=n5,B Step 7. Two extra equations - recoveries - are related to the distillation column. n3,An4,A=10083.1n4,En3,E=10059.2 Step 8. Five unknowns are: n4,A,n4,E,n5,A,n5,E,n5,B Step 9. Five unknowns match five equations. Therefore, the system can be solved, and no additional systems are needed (Step 10). Step 11. The B mole balance can be quickly solved, then the extra equations provide flow rates that are used to solve the A and E mole balances. n3,B=n5,B=204minmoln3,An4,A=10083.1n4,A=3.70E+2minmol10083.1n4,A=n3,A=n4,A+