I Want this code in C language , if you are expert in C++ do it in C++

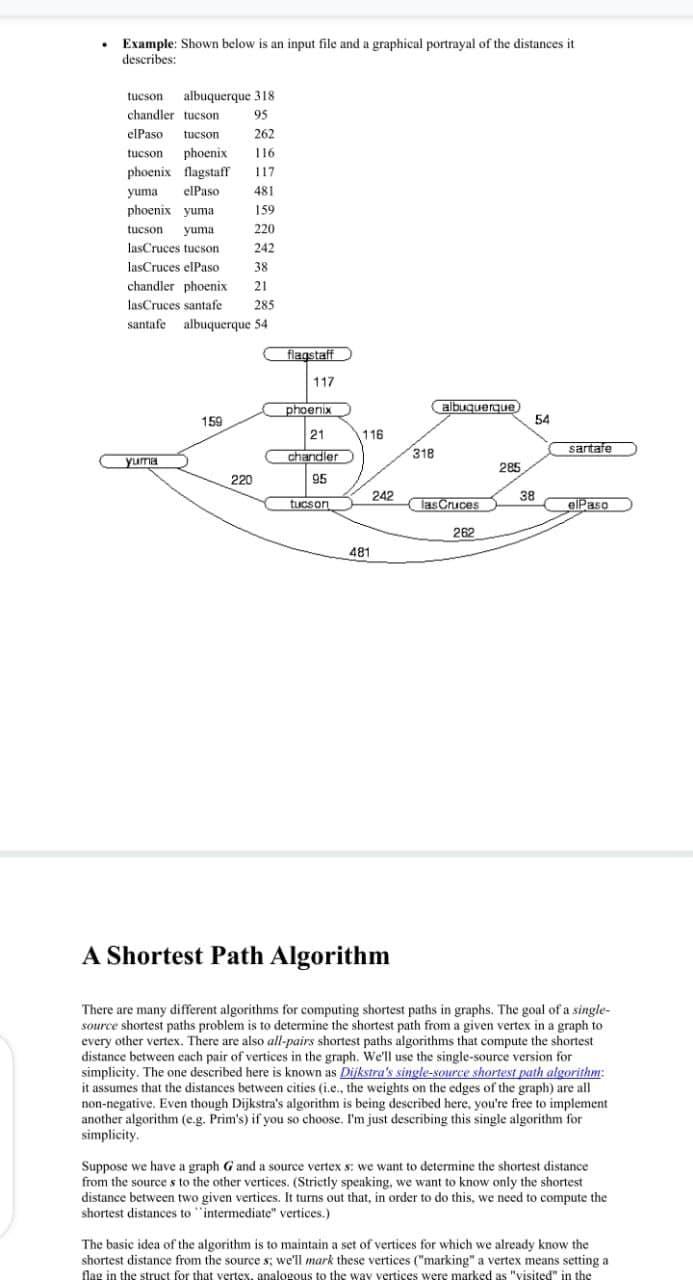
The purpose of this assignment is to to work with linked lists, memory allocation, representing a graph in c, command line arguments, reading from a file, and using free). General Requirements 1. Your C code should adhere to the coding standards for this class as listed in the Documents section on the Resources tab for Piazza. This includes protecting against buffer overflows whenever you read strings. 2. Your programs should indicate if they executed without any problems via their exit status, i.e., the value returned by the program when it terminates: Execution Exit Status Normal, no problems 0 Error or problem encountered 1 3. Under bash you can check the exit status of a command or program emd by typing the command "echo $?" immediately after the execution of cmd. A program can exit with status n by executing "exit (n)" anywhere in the program, or by having main() execute the statement "return(n)". 4. To get full points your code should compile without warnings or errors when the-Wall flag is set in gee 5. You must check the return values to system calls that might fail due to not being able to allocate memory, (e.g. Check that malloc/calloc don't return NULL) getline() is an exception to this rule. 6. Your code must run without errors using valgrind meaning that valgrind shows the line "ERROR SUMMARY:0 errors" for all test cases, 7. New Requirement: You must free all your memory before exiting to get full credit. Problems probl: shortest Paths This problem can be thought of, conceptually, as an elaboration of a previous programming problem involving reachability in graphs, i.e., determining whether there is a path between two vertices in an undirected graph (however, the actual programming is quite different in many respects). In this case, we assume that the input graph is connected, that edges have weights ("distances") associated with them, and our goal is to compute the shortest distance between two cities. Terminology: For the purposes of this problem, a name is a string, consisting of upper and lower case letters only, of length at most 64 (See man isalpha). A query is a pair of names separated by whitespace. Write a C program in a file shortest Paths.e together with a Makefile that creates an executable shortest Paths which behaves as specified below. Invocation: Your program will be invoked with a single command-line argument: shortest Paths inFile where "inFile" is the name of a file which contains the description of the undirected graph. Behavior: After reading the file giving distances between cities, your program will repeatedly perform the following computation: 1. read in a query from stdin, 2. compute the shortest distance between the two names specified in the query; and 3. print the distance so computed to stdout according to the format specified below. until no further input can be read. Input: 1. Input File Format: The input file consists of a series of lines where each line has the form name: name2 disti2 where name, and name are names and disti2 is the distance between them. disti2 should be a non-negative integer. These arguments are separated by white space. Note each line describes an edge between two vertices. Since this is an indirected graph, the order of the names doesn't matter. 2. Query Formar: Each query is on a separate line and is a pair of names separated by whitespace. (See above under "Terminology":) Assumptions: You can assume the following: 1. Each name read in either from the input file (as part of the distance database) or from stdin (as part of a query) has length at most 64. As always, you still need to protect against buffer overflows. 2. The graph described by the input file is connected. . Output: Output should be printed to stdout using the statement printf("4d ", val) where val is the value computed as the shortest distance between a pair of cities. . Error Conditions: 1. Fatal errors: Not enough command line arguments or input file cannot be opened for reading. 2. Non-fatal errors Anything that does not meet the specification given above but is not a fatal error. Since the error is not fatal, your program should do something sensible (but give an appropriate error message) and continue execution. Examples (this is not an exhaustive list): too many command-line arguments (ignore extra arguments), input line not in the format specified (ignore the offending line): distance between some pair of cities is specified multiple times (ignore all but the first); city names) read from stdin not in the distance database read from the input file (ignore that input line). As always, if you wonder if something should be considered to be an error experiment with the example executable. Example: Shown below is an input file and a graphical portrayal of the distances it describes: tucson albuquerque 318 chandler tucson 95 elPaso tucson 262 tucson phoenix 116 phoenix Magstaff 117 yuma elPaso 481 phoenix yuma 159 tucson yuma 220 lasCruces tucson 242 lasCruces e Paso 38 chandler phoenix 21 latsCruces santafe 285 santafe albuquerque 54 flagstaff 117 phoenix albuquerque 159 54 21 116 chandler 318 sartare yum 285 220 95 242 38 tucson las Cruces elPaso 262 481 A Shortest Path Algorithm There are many different algorithms for computing shortest paths in graphs. The goal of a single- source shortest paths problem is to determine the shortest path from a given vertex in a graph to every other vertex. There are also all-pairs shortest paths algorithms that compute the shortest distance between ench pair of vertices in the graph. We'll use the single-source version for simplicity. The one described here is known as Dijkstra's single-source shortest path algorithm: it assumes that the distances between cities (ie, the weights on the edges of the graph) are all non-negative. Even though Dijkstra's algorithm is being described here, you're free to implement another algorithm (e.g. Prim's) if you so choose. I'm just describing this single algorithm for simplicity Suppose we have a graph G and a source vertex so we want to determine the shortest distance from the source s to the other vertices. (Strictly speaking, we want to know only the shortest distance between two given vertices. It turns out that, in order to do this, we need to compute the shortest distances to intermediate" vertices.) The basic idea of the algorithm is to maintain a set of vertices for which we already know the shortest distance from the sources, we'll mark these vertices ("marking" a vertex means setting a flag in the struct for that vertex, analogous to the way vertices were marked as "visited in the reachability problem). As the algorithm executes, therefore, we have two classes of vertices: A set of marked vertices: for each such vertex a, we know the exact value of the shortest distance from the sources to a The remaining vertices, which are unmarked: for each such vertex a, we have an upper bound approximation d(a) to the shortest distance from the source s to a "Upper bound approximation" means that we may not know the exact shortest distance from s to a, but we know that this distance is at most d(a). The essential idea in the algorithm is to iterate over the vertices in the graph: in each iteration we are able to take an unmarked vertex and compute the exact shortest distance to it. The algorithm terminates when all vertices are marked (assuming that the graph is connected). Data Structures The data structure for this is in many ways similar to that for the graph reachability problem, with the following differences: 1. Each edge e now has an additional field dist, an integer, which gives the value of the distance between the two endpoints of that edge. 2. Each vertex y now has an additional field min Dist, an integer that gives the shortest distance from the source to that vertex. 3. The graph is undirected, so every time you add an edge from A to B, add an identical edge from B to A. Initialization Initially, all we can say about the shortest distances is that the shortest distance from the source vertex to itself is 0. For all the other vertices, we set the min Dist field to infinity (actually, to INT_MAX). Thus, this phase looks like: for each vertex vt v.minist = INT MAX; unmarkvi sre.indist = 0; Iteration The main idea in the iteration is to find, at each iteration, a vertex u to which we already know the exact shortest distance from the source (as mentioned in the Initialization phase above, initially the only such vertex is the source itself), then use this to improve our estimate of the min Dist field of all of the neighbors of u. Suppose that a vertex v is a neighbor of w, where e is the edge between u and y, Now v.min Dist is our current approximation to the shortest distance from the source to v. Suppose that we find that u.minDist + e.dist 0 for all edges e, this means that if wis an unmarked vertex with the smallest min Dist value of all the unmarked vertices, then its value can't get any smaller. So we can mark the vertex w. i.e., conclude that we've found the shortest distance from the source to w. (Actually, during each round of iteration we do this step first, then update the min Dist fields of w's neighbors: this is discussed below.) The purpose of this assignment is to to work with linked lists, memory allocation, representing a graph in c, command line arguments, reading from a file, and using free). General Requirements 1. Your C code should adhere to the coding standards for this class as listed in the Documents section on the Resources tab for Piazza. This includes protecting against buffer overflows whenever you read strings. 2. Your programs should indicate if they executed without any problems via their exit status, i.e., the value returned by the program when it terminates: Execution Exit Status Normal, no problems 0 Error or problem encountered 1 3. Under bash you can check the exit status of a command or program emd by typing the command "echo $?" immediately after the execution of cmd. A program can exit with status n by executing "exit (n)" anywhere in the program, or by having main() execute the statement "return(n)". 4. To get full points your code should compile without warnings or errors when the-Wall flag is set in gee 5. You must check the return values to system calls that might fail due to not being able to allocate memory, (e.g. Check that malloc/calloc don't return NULL) getline() is an exception to this rule. 6. Your code must run without errors using valgrind meaning that valgrind shows the line "ERROR SUMMARY:0 errors" for all test cases, 7. New Requirement: You must free all your memory before exiting to get full credit. Problems probl: shortest Paths This problem can be thought of, conceptually, as an elaboration of a previous programming problem involving reachability in graphs, i.e., determining whether there is a path between two vertices in an undirected graph (however, the actual programming is quite different in many respects). In this case, we assume that the input graph is connected, that edges have weights ("distances") associated with them, and our goal is to compute the shortest distance between two cities. Terminology: For the purposes of this problem, a name is a string, consisting of upper and lower case letters only, of length at most 64 (See man isalpha). A query is a pair of names separated by whitespace. Write a C program in a file shortest Paths.e together with a Makefile that creates an executable shortest Paths which behaves as specified below. Invocation: Your program will be invoked with a single command-line argument: shortest Paths inFile where "inFile" is the name of a file which contains the description of the undirected graph. Behavior: After reading the file giving distances between cities, your program will repeatedly perform the following computation: 1. read in a query from stdin, 2. compute the shortest distance between the two names specified in the query; and 3. print the distance so computed to stdout according to the format specified below. until no further input can be read. Input: 1. Input File Format: The input file consists of a series of lines where each line has the form name: name2 disti2 where name, and name are names and disti2 is the distance between them. disti2 should be a non-negative integer. These arguments are separated by white space. Note each line describes an edge between two vertices. Since this is an indirected graph, the order of the names doesn't matter. 2. Query Formar: Each query is on a separate line and is a pair of names separated by whitespace. (See above under "Terminology":) Assumptions: You can assume the following: 1. Each name read in either from the input file (as part of the distance database) or from stdin (as part of a query) has length at most 64. As always, you still need to protect against buffer overflows. 2. The graph described by the input file is connected. . Output: Output should be printed to stdout using the statement printf("4d ", val) where val is the value computed as the shortest distance between a pair of cities. . Error Conditions: 1. Fatal errors: Not enough command line arguments or input file cannot be opened for reading. 2. Non-fatal errors Anything that does not meet the specification given above but is not a fatal error. Since the error is not fatal, your program should do something sensible (but give an appropriate error message) and continue execution. Examples (this is not an exhaustive list): too many command-line arguments (ignore extra arguments), input line not in the format specified (ignore the offending line): distance between some pair of cities is specified multiple times (ignore all but the first); city names) read from stdin not in the distance database read from the input file (ignore that input line). As always, if you wonder if something should be considered to be an error experiment with the example executable. Example: Shown below is an input file and a graphical portrayal of the distances it describes: tucson albuquerque 318 chandler tucson 95 elPaso tucson 262 tucson phoenix 116 phoenix Magstaff 117 yuma elPaso 481 phoenix yuma 159 tucson yuma 220 lasCruces tucson 242 lasCruces e Paso 38 chandler phoenix 21 latsCruces santafe 285 santafe albuquerque 54 flagstaff 117 phoenix albuquerque 159 54 21 116 chandler 318 sartare yum 285 220 95 242 38 tucson las Cruces elPaso 262 481 A Shortest Path Algorithm There are many different algorithms for computing shortest paths in graphs. The goal of a single- source shortest paths problem is to determine the shortest path from a given vertex in a graph to every other vertex. There are also all-pairs shortest paths algorithms that compute the shortest distance between ench pair of vertices in the graph. We'll use the single-source version for simplicity. The one described here is known as Dijkstra's single-source shortest path algorithm: it assumes that the distances between cities (ie, the weights on the edges of the graph) are all non-negative. Even though Dijkstra's algorithm is being described here, you're free to implement another algorithm (e.g. Prim's) if you so choose. I'm just describing this single algorithm for simplicity Suppose we have a graph G and a source vertex so we want to determine the shortest distance from the source s to the other vertices. (Strictly speaking, we want to know only the shortest distance between two given vertices. It turns out that, in order to do this, we need to compute the shortest distances to intermediate" vertices.) The basic idea of the algorithm is to maintain a set of vertices for which we already know the shortest distance from the sources, we'll mark these vertices ("marking" a vertex means setting a flag in the struct for that vertex, analogous to the way vertices were marked as "visited in the reachability problem). As the algorithm executes, therefore, we have two classes of vertices: A set of marked vertices: for each such vertex a, we know the exact value of the shortest distance from the sources to a The remaining vertices, which are unmarked: for each such vertex a, we have an upper bound approximation d(a) to the shortest distance from the source s to a "Upper bound approximation" means that we may not know the exact shortest distance from s to a, but we know that this distance is at most d(a). The essential idea in the algorithm is to iterate over the vertices in the graph: in each iteration we are able to take an unmarked vertex and compute the exact shortest distance to it. The algorithm terminates when all vertices are marked (assuming that the graph is connected). Data Structures The data structure for this is in many ways similar to that for the graph reachability problem, with the following differences: 1. Each edge e now has an additional field dist, an integer, which gives the value of the distance between the two endpoints of that edge. 2. Each vertex y now has an additional field min Dist, an integer that gives the shortest distance from the source to that vertex. 3. The graph is undirected, so every time you add an edge from A to B, add an identical edge from B to A. Initialization Initially, all we can say about the shortest distances is that the shortest distance from the source vertex to itself is 0. For all the other vertices, we set the min Dist field to infinity (actually, to INT_MAX). Thus, this phase looks like: for each vertex vt v.minist = INT MAX; unmarkvi sre.indist = 0; Iteration The main idea in the iteration is to find, at each iteration, a vertex u to which we already know the exact shortest distance from the source (as mentioned in the Initialization phase above, initially the only such vertex is the source itself), then use this to improve our estimate of the min Dist field of all of the neighbors of u. Suppose that a vertex v is a neighbor of w, where e is the edge between u and y, Now v.min Dist is our current approximation to the shortest distance from the source to v. Suppose that we find that u.minDist + e.dist 0 for all edges e, this means that if wis an unmarked vertex with the smallest min Dist value of all the unmarked vertices, then its value can't get any smaller. So we can mark the vertex w. i.e., conclude that we've found the shortest distance from the source to w. (Actually, during each round of iteration we do this step first, then update the min Dist fields of w's neighbors: this is discussed below.)