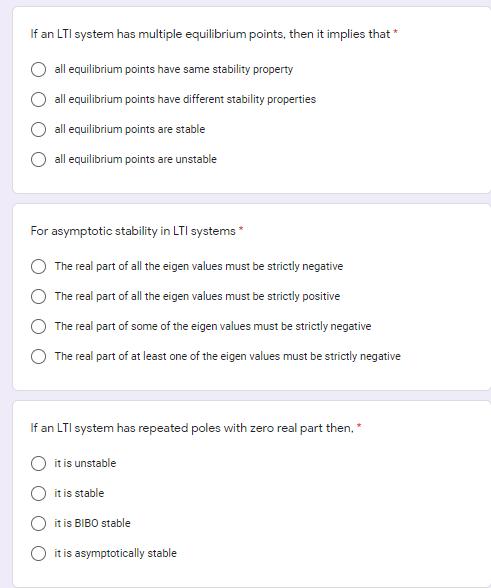
If an LTI system has multiple equilibrium points, then it implies that* all equilibrium points have same stability property O all equilibrium points have different stability properties all equilibrium points are stable all equilibrium points are unstable For asymptotic stability in LTI systems * The real part of all the eigen values must be strictly negative The real part of all the eigen values must be strictly positive The real part of some of the eigen values must be strictly negative The real part of at least one of the eigen values must be strictly negative If an LTI system has repeated poles with zero real part then,* it is unstable it is stable it is BIBO stable it is asymptotically stable