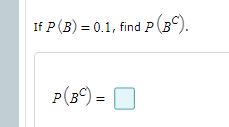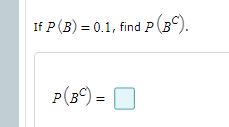
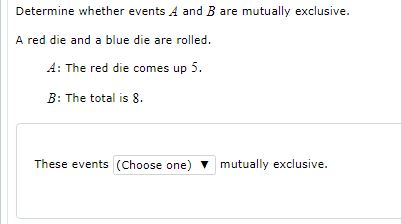




If P(A) = 0.51, P(B) = 0.7, and P(4 and B) = 0.41, find P (A or B). P(A or B =Sick children: There are 20 students in Mrs. Bush's sixth-grade class. On a cold winter day in February, many of the students had runny noses and sore throats. After examining each student, the school nurse constructed the following table. Round the answers to four decimal places, as needed. Sore Throat No Sore Throat Runny Nose 10 No Runny 4 Nose Send data to Excel (a) Find the probability that a randomly selected student has a runny nose. (b) Find the probability that a randomly selected student has a sore throat, (c) Find the probability that a randomly selected student has a runny nose or a sore throat. (d) Find the probability that a randomly selected student has neither runny nose nor a sore throat. Part 1 of 4 (=) Find the probability that a randomly selected student has a runny nose. The probability that a randomly selected student has a runny nose is Part 2 of 4 (b) Find the probability that a randomly selected student has a sore throat. The probability that a randomly selected student has a sore throat is Part 3 of 4 (c) Find the probability that a randomly selected student has a runny nose or a sore throat. The probability that a randomly selected student has a runny nose or sore throat is Part 4 of 4 (d) Find the probability that a randomly selected student has neither runny nose nor a sore throat. The probability that a randomly selected student has neither runny nose nor a sore throat isIf P(A) = 0.7, P(B) =0.2, and A and B are mutually exclusive, find P (A or B). P( A or B) = X 5If P(A) =0.3, P(B) = 0.3, and P(A or B) =0.6 are A and B mutually exclusive? A and B (Choose one) mutually exclusive.If P (B) = 0.1, find P (B")Determine whether events A and B are mutually exclusive. A red die and a blue die are rolled. A: "I11e red die comes up 5. B: 111e total is E. 111ese events {Chinese one] If mutuallyr exclusive. A sample of 21 notebook computers was selected. Find the complements of the following event Part 1 of 4 Exactly S of the notebook computers weigh less than 3 pounds. The complement is: The number of notebook computers weighing less than 5 pounds is (Choose one) Part 2 of 4 At least 5 of the notebook computers weigh less than 5 pounds. The complement is: (Choose one) v notebook computers weigh less than 3 pounds. Part 3 of 4 More than 5 of the notebook computers weigh less than 5 pounds. The complement is: (Choose one) v notebook computers weigh less than 3 pounds. Part 4 of 4 Fewer than 5 of the notebook computers weigh less than 5 pounds. The complement is: (Choose one) v notebook computers weigh less than 5 pounds.Car repairs: Let _ be the event that a new car requires engine work under warranty and let /" be the event that the car requires transmission work under warranty. Suppose that P (E) = 0.09, P(7 ) =0.08, P(E and 7 ) = 0.06. (a) Find the probability that the car needs work on either the engine, the transmission, or both. (b) Find the probability that the car needs no work on the transmission. Part 1 of 2 (a) Find the probability that the car needs work on either the engine, the transmission, or both. The probability that the car needs work on either the engine, the transmission, or both is Part 2 of 2 (b) Find the probability that the car needs no work on the transmission. The probability that the car needs no work on the transmission isComputer purchases: Out of 794 large purchases made at a computer retailer, 333 were personal computers, 391 were laptop computers, and 70 were printers. As a part of an audit, one purchase record is sampled at random. Round the answers to four decimal places, as needed. (a) What is the probability that it is a laptop computer? (b) What is the probability that it is not a printer? Part 1 of 2 (a) What is the probability that it is a laptop computer? The probability that it is a laptop computer is Part 2 of 2 (b) What is the probability that it is not a printer? The probability that it is not a printer isVisit your local library: On a recent Saturday, a total of 1314 people visited a local library. Of these people, 247 were under age 10, 451 were aged 10-18, 164 were aged 19-30, and the rest were more than 30 years old. One person is sampled at random. (a) What is the probability that the person is less than 10 years old? (b) What is the probability that the person is more than 30 years old? Part 1 of 2 (a) What is the probability that the person is less than 10 years old? Round your answer to four decimal places. The probability that the person is less than 10 years old is Part 2 of 2 (b) What is the probability that the person is more than 30 years old? Round your answer to four decimal places. The probability that the person is more than 30 years old is