Question: Iff: 2- is defined by f(x, y) = xy/(x + y) unless x that D.f(0, 0) exists for all v, but f is not

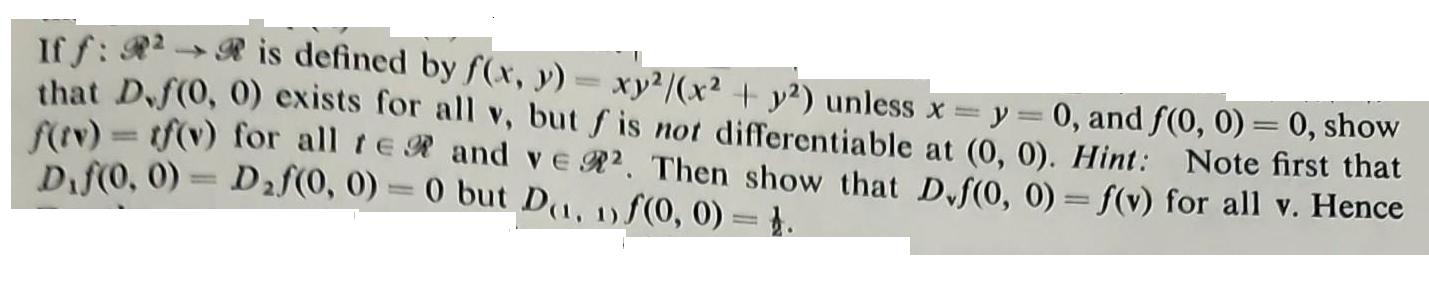
Iff: 2- is defined by f(x, y) = xy/(x + y) unless x that D.f(0, 0) exists for all v, but f is not differentiable at (0, 0). Hint: Note first that f(tv) = tf(v) for all te and ve . Then show that D.f(0, 0) = f(v) for all v. Hence y = 0, and f(0, 0) = 0, show Dif(0,0) - Df(0, 0) = 0 but D(1, 1)f(0, 0) = 4.

Step by Step Solution

★★★★★

3.43 Rating (162 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock

To show that Df0 0 exists for all v but f is not differentiable at 0 0 we can follow the given hints ... View full answer

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Mathematics Questions!

Show there does not exist a continuously differentiable function f on [0, 2] such that f(0) = -1, f(2) = 4, and f(x)

Show that for any continuous even function f defined on the interval [a, a], we have jaa f (x) dx =

Show that the function f defined by f (x) := x = x/x2 + 1; x R, is a bijection of R onto {y : 1

Consider the function f : R2 - R defined by f (x, y) = ry 1 2 ty (x, y) # (0, 0) (x, y) = (0,0) (a) (6 points) Calculate fr and fy, and show that one of them is continuous (both are continuous, but...

854 CHAPTER 15 DIFFERENTIATION IN SEVERAL VARIABLES 9. 20. Jessica and I at 2 oh ; h (x , y ) = -, x = 1/2, y = 1712 paths that make a with velocity va 10. "J : f ( x , y , Z ) = xy - 22, x = rcos0,...

Problem 2 Neglecting radiation, there is fully-developed forced convection through a cylindrical pipe with a uniform wall heat flux q". The pipe's radius is R, the pipe's length is L, the mass...

Kindly give only correct answers showing your steps 1. (a) Use the Intermediate Value Theorem to show that the equation - sin (x) + sin(x) =-1 has at least two distinct real solutions on (0, ce)....

Letkbe a real number. DefinefR2R2by ((x2+y2)k,x22k)ifx0,2kLetkbe a real number. DefinefR2R2by ((x2+y2)k,x22k)ifx0,2k f(x,y)= (y ,k)ifx=0andy0,(0,k)ifx=y=0. Find the value ofkfor whichfis...

(c) A inction at, y) is dierentiable at (a, b) if and only if the linear approximation is a good approxi- mation of the function near the point (a, b). In other words, the surface 2 = f(l':, 3;) near...

here are the questions. Thank you (a) Let f | D - R be a real valued function from R" to R with domain D in R", n > 2. Given a E D, define the directional derivative of f at a in the direction u,...

Describe the rights and responsibilities of auditors under: a) Legislation b) Decisions of the courts c) Auditing standards d) Other regulatory requirements - in particular, those relating to listed...

Using the diagram of the risk-return curve and the capital market line, explain how having a banking system in the economy improves investment opportunities.

A B C D E F G H J K 1 Requirement #1: 2 During its first month of operation, the True Consulting Corporation, which specializes in management consulting, 3 completed the following transactions. 4 5...

Describe your target audience for your project and identify whether they are beginners or experts. Determine a sequencing strategy for your project and provide a rationale for your selection. Include...

Do you agree with the author's questioning of the goodness of this way of life? Explain your answer.

For the plane structures shown in Figure Q1, check for stability, and determine the degree of statical indeterminacy. (a) (b) (c) (d) (e) (f) (g) 12:42 AM 8 ^ ) ENG 2020/09/05 LILLI

Exercise 4. The inside radius of a small test tube can be determine using the following method. Fill the test tube nearly to the top with water (refer to Figure 1). The height, h, of the water level...

The bookkeeper of Balamu Enterprises found the following during a bank reconcilation exercise during Apeil 2017: March 2017 Bank statement Outstanding Cheque CC021 Cheque CC0B7 Deposit Cheque CC089...

Which of the following elements are included in separation costs ( Choose all that apply ) ? Multiple select question. exit interview market - based pay separation pay administrative functions...

If r(t) = (t, t 2 , t 3) , find r'(t), T(1), r'(t), and r''(t) x r'(t).

Compute the outward flux of F(x, y, z) = x i + y j + z k/(x 2 + y 2 + z 2 ) 3/2 through the ellipsoid 4x 2 + 9y 2 + 6z 2 = 36.

Find the area of the region bounded by the given curves. tan?x, , 0

In Canada, the health and safety of workers are protected by the Occupational Health and Safety Act of each province, which is enforced by the ministry (or department) of Labour of the province. For...

In an initial survey designed to estimate the percentage of time air-express cargo loaders are idle, an analyst found that loaders were idle in 6 of the 50 observations. a. What is tire estimated...

Develop a standard time for preparing a ham and cheese sandwich: a. List the steps (tasks) required to prepare the sandwich. b. Observe tire job for several repetitions and make improvements if...