Imagine you are the network administrator in charge of a huge communication network. The network can be modeled as a directed graph G = (V, E).
There are n friends, each of whom requests for a specific simple path Pi, i = 1, 2, · · · n in the network. You are willing to allocate as many paths as you can.
However, here is the catch - if you allocate the paths requested by friends i and j, then you have to make sure that Pi and
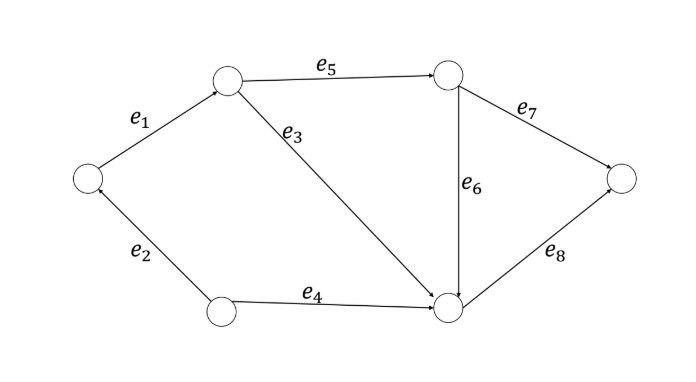
Pj does not pass through a common node in the network. In the example below, say P1 = {e1, e5}, P2 = {e4, e8}, P3 = {e1, e3, e8}. Here, you can
allocate P1 and P2. Note that if you allocate P3, then you cannot allocate either P1 or P2. So here is the question you are pondering over - given an integer k,
can I satisfy at least k of my friends under the given constraints?
Prove the above problem in NP-Complete.
a) First prove that the above problem is in NP.

b) Given a polynomial-time reduction from Independent Set (IS) to your problem - Given any instance of IS, you need to construct an instance of the given problem in
polynomial time (remember to specify all parameters of the instance in your construction).

c) Prove that YES instance for IS implies the corresponding instance for the given problem is also YES.
d) Prove that YES instance for your problem implies the corresponding instance for IS is also YES.

 

e e2 3 e5 e4 e6 e7 eg