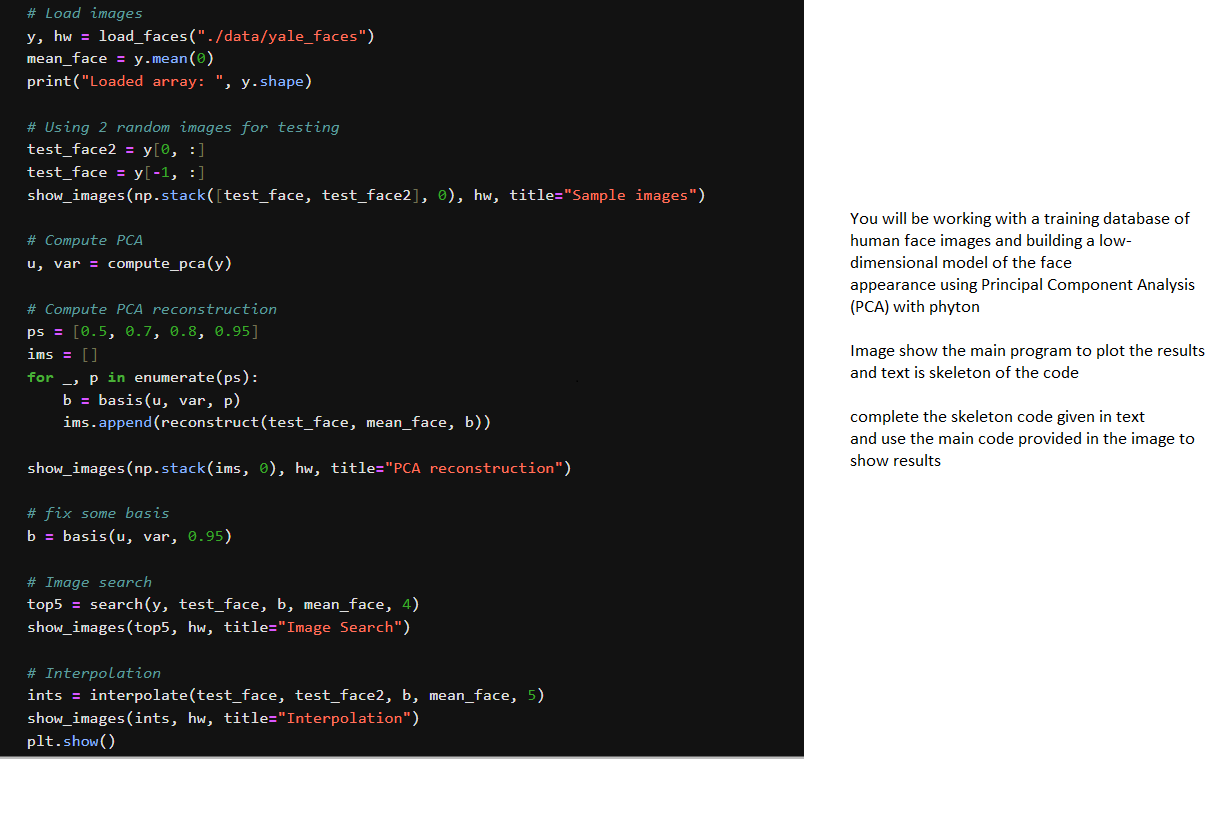
import numpy as np

import os

from PIL import Image

def load$\_$faces$($path$,$ ext$=".$pgm$")$:

$"""$Load faces into an array $($N$,$ M$),$

where N is the number of face images and M is the dimensionality

$($height$*$width for greyscale$).$

Hint: os$.$walk$()$ supports recursive listing of files

and directories in a path

Args:

path: path to the directory with face images

ext: extension of the image files $($you can assume $.$pgm only$)$

Returns:

x: $($N$,$ M$)$ array

hw: $($H$,$ W$)$ tuple

$"""$

#

# You code here

#

def PCA$\_$mcq$()$:

$"""$

Which method will be a more reasonable choice in your implementation

$0$: SVD

$1$: Eigendecomposition

Why?

$0$: It is more computationally efficient for our problem

$1$: It allows to compute eigenvectors and eigenvalues of any matrix

$2$: It can be applied to any matrix and is more numerically stable

$3$: We can find the eigenvalues we need for our problem from the singular values

$4$: We can find the singular values we need for our problem from the eigenvalues

Return your answer as a tuple, e$.$g$.,$ return $(0,0,1)$ means that the more reasonable

method is SVD because it is more computationally efficient for our problem, and

allows to compute eigenvector and eigenvalues of any matrix.

$"""$

return

def compute$\_$pca$($X$)$:

$"""$PCA implementation

Args:

X: $($N$,$ M$)$ an array with N M$-$dimensional features

Returns:

u: $($M$,$ M$)$ bases with principal components

var: $($N$,)$ corresponding variance

$"""$

#

# You code here

#

def basis$($u$,$ var, p$=0\mathrm{.}5)$:

$"""$Return the minimum number of basis vectors from matrix U such

that they account for at least p percent of total variance.

Hint: Do the singular values really represent the variance?

Args:

u: $($M$,$ M$)$ numpy array containing principal components.

For example, i'th vector is u$[$:$,$ i$]$

var: $($N$,)$ numpy array containing the variance along the principal components.

p: percent of total variance that should be contained.

Returns:

v: $($M$,$ D$)$ numpy array that contains M principal components containing at most

p $($percentile$)$ of the variance.

$"""$

#

# You code here

#

def reconstruct$($face$\_$image, mean$\_$face, u$)$:

$"""$Reconstructs the face image with respect to the first D

principal components u$.$

Args:

face$\_$image: $($M$,)$ numpy array $($M$=$H$*$W$)$ of the face.

mean$\_$face: $($M$,)$ numpy array $($M$=$H$*$W$)$ mean face.

u: $($M$,$ D$)$ matrix containing D principal components.

Returns:

reconstructed$\_$img: $($M$,)$ numpy array of reconstructed face image

$"""$

#

# You code here

#

def components$\_$mcq$()$:

$"""$

Select the right answer $($only one option$)$:

$0$: The first principal components mostly correspond to local features, e$.$g$.,$ nose, mouth, eyes

$1$: The first principal components predominantly contain global structure, e$.$g$.,$ complete face

$2$: The fewer principal components we use, the smaller is the re$-$projection error

$3$: The more principal components we use, the sharper is the image

$4$: The variations in the last principal components is perceptually insignificant; these bases can be neglected in the projection

$"""$

return

def search$($Y$,$ x$,$ u$,$ mean$\_$face, top$\_$n$)$:

$"""$Search for the top most similar images based on a given number of

components in their PCA decomposition.

Args:

Y: $($N$,$ M$)$ numpy array with N M$-$dimensional features

x: $($M$,)$ numpy array image we would like to retrieve

u: $($M$,$ D$)$ numpy arrray, bases vectors. Note, we already assume D has been selected

mean$\_$face: $($M$,)$ numpy array, mean face as a vector

top$\_$n: integer, number of n closest images using L$2$ distance to return

Returns:

Y: $($top$\_$n$,$ M$)$

$"""$

#

# You code here

#

def interpolate$($x$1,$ x$2,$ u$,$ mean$\_$face, n$)$:

$"""$Interpolates from x$1$ to x$2.$

Args:

x$1$: $($M$,)$ numpy array, the first image

x$2$: $($M$,)$ numpy array, the second image

u: $($M$,$ D$)$ numpy array, bases vectors. Note, we already assume D has been selected.

mean$\_$face: $($M$,)$ numpy array, mean face as a vector

n: number of interpolation steps $($including x$1$ and x$2)$

Hint: you can use np$.$linspace to generate N equally$-$spaced points on a line

SEE Returns:

Y: $($n$,$ M$)$ numpy arrray, interpolated results.

The first dimension is in the index into corresponding

image; Y$[0]==$ reconstruct$($x$1,$ mean$\_$face, u$)$; Y$[-1]==$ reconstruct$($x$2,$ mean$\_$face, u$)$

$"""$

#

# You code here

#