*(Important Note) Please explain thoroughly and show your work in each question including how you get the mean, standard deviation and the sketches with your data. No rush and take your time to get your answer correct Note: this is a two-part project. Part 1 Obtain data that is quantitative and continuous. The data gathered must be relevant to something that is of interest to you. Once this data is obtained, you will need to analyze it using strategies/tools we have discussed in class. You can collect data by creating and conducting your own survey that produces quantitative/continuous data or by finding data from a reputable source. If you find the data from a reputable source, it can't be data that has already been analyzed. There are data finding resources available at the end of this document if you wish to use those. There are more details regarding data analysis in the "what will make up your grade" portion of the assignment. Please read all requirements specified in "what will make up your grade" before you being the project. You can use these items and fill in your responses below them, rather than writing this essay style. Purpose: The purpose of this project is to apply what we have learned in context. Being able to analyze data in a basic sense and understand data that has been analyzed is crucial, nowadays. We are regularly subject to information via social media, news, etc. that discusses data analysis (even if it is at a basic level). It is becoming highly common to use basic data analysis to assess things like performance and productivity in the work place. This is true even for non "math" or "STEM" based fields. It is something we all need to have a basic level of understanding in to be informed consumers of information. What will make up your grade: 1. (3 points) The data you chose to explore is quantitative and continuous. You will be expected to explain how you know this is both quantitative and continuous. 2. (2 points) Please explain if your data results are from an observational or experimental study and why. 3. (3 points) You are exploring something you are interested in. To earn credit, explain why you are interested in this topic that you gathered data about. 4. (2 points) You collect at least 20 data values. More specifically, give your survey to at least 20 people or find a source that gives at least 20 non-analyzed data values. Note that non-analyzed means the calculations/graphs in this project have not already been done for you by the source you obtained the data from. Record the raw data you obtain. Meaning list the data in your project. 5. (5 points) Make a histogram or stem and leaf plot for your data. You are welcome to use an online histogram calculator if desired. For the histogram, I will be grading on the criteria of it having a title, correct vertical axis label, correct horizontal axis label, equal bar lengths that show the skew of your data, and that all data is included. For the stem and leaf plot, all data must be displayed consistently in the "stem" and "leaf" segments (as seen in class) and labels much be included. Note that this is being done so you will be able to discuss the skew of the data.

6. (3 points) Discuss the skew of the data based on your histogram. In this discussion of skew you will need to use vocabulary from class. 7. (7 points) Calculate and record the five-number summary for your data. You may use your calculator for this, but I encourage you to show some work too. Showing work demonstrates understanding and guards you from not earning full credit due to a data entry error. 8. (10 points) Calculate and record the mean and standard deviation for your data. Again, you may use your calculator, but I encourage you to show some work too. Showing work demonstrates understanding and guards you from not earning full credit due to a data entry error. 9. (10 points) After calculating both the mean/standard deviation and the 5 number-summary, state which is stronger in giving a more accurate summary of your data. Explain why this is true using the concepts of skewness and outliers. Meaning, use objective reasoning that has been discussed in class to answer this question. Do not use subjective opinion about which measure looks better to you. Note: Keep in mind that to explain using the concept of outliers, it is necessary to test for them to determine if you have any. To earn full credit in this section, you must show your work for this outlier test. 10. (5 points) Summarize the study results. In this summary discuss what the skew, outliers, and summary measures (mean/standard deviation and the five-number summary) mean in context. In context mean in the real-life scenario of this data. Other questions to answer in this summary are: (1) What does the data tell you about the question you asked? (2) Is this surprising to you or consistent with what you would have expected? (3) Can you think of any variables that may confound the study or results? As I would expect for any project, make sure your project is well written. It should be clearly and neatly written (by hand is fine if that is a better means for you) or typed. Each topic addressed above can serve as a heading for each point you are making. Data Resources Here are some resources if you decide to gather data from an outside source rather than conduct a survey. These resources are not extensive, meaning you can gather data from elsewhere. Please be aware that it may take some time and some digging around on these sites to find something that will be both quantitative and continuous, and be of interest. Also be mindful of how many variables our data analysis/summary techniques in this project are meant to represent. Climate Data Note for this data, you will need to use the time series graphs to obtain data values. What you could do is build a histogram to consider the data values over a certain period of time, for example each year for a set amount of 20 years if you want 20 data values. When doing this, you should be mindful of how many variables histograms are meant to represent, the form they take, and set it up appropriately from the link below. ? https://climate.nasa.gov/vital-signs/carbon-dioxide/?intent=121 ? https://climate.nasa.gov/vital-signs/global-temperature/?intent=121

https://climate.nasa.gov/vital-signs/arctic-sea-ice/?intent=121 ?https://climate.nasa.gov/vital-signs/ice-sheets/?intent=121 ?https://climate.nasa.gov/vital-signs/sea-level/?intent=121 ?

Data on Occurrences in the US Population (good for exploring social occurrences): https://ephtracking.cdc.gov/ PEW Research Center Data Sets (various types)https://www.pewresearch.org/datasets/ An Assortment of Data Resources from https://www.whatcom.edu/student-services/tutoring-learning-center/online-math-center/resources/real-data

Data from our course material that you can find in the course notes (1) VAERS data (2)Public employee salary data.

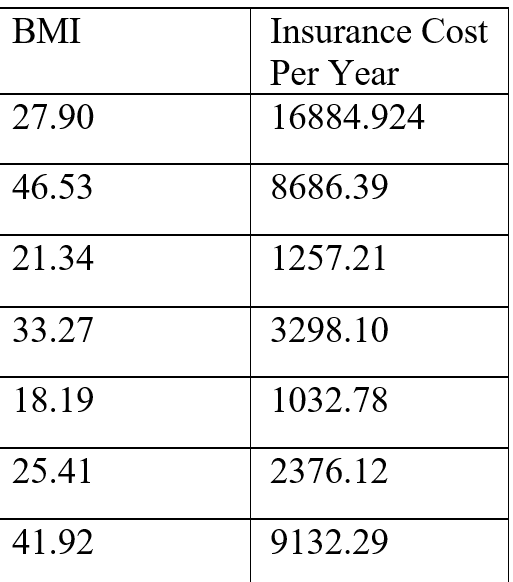
Part 2 In this portion of the project I will be giving a data set, and you will need to answer various questions about it. The purpose of this is to allow us to consider multiple variables, and draw conclusions using concepts of skewness and regression. The data set we will use discusses insurance costs based on multiple variables. Here is the data set you will need to use to answer all questions below https://www.kaggle.com/datasets/mirichoi0218/insurance. Note that this data set is communicating that the variables displayed are predictors of insurance charges. 1. In the data set, you will see histograms at the top of the columns for the variables age, BMI, children, insurance charges. You will need to interpret what those histograms mean by discussing their skew. a. Age histogram - what skew does this histogram have? What does that mean about the ages of the people studied? b. BMI histogram - why skew does this histogram have? What is the approximate center of the histogram (you do not need to calculate this, you can look at the histogram)? What does this mean about the BMIs of the people studied? c. Number of children - what skew does this histogram have? What does that mean about the number of children people in the study had? d. Charges - what skew does this histogram have? Why does this skewness make sense in a real-world context? When answering this, consider peaks and why that would make sense in the real world. 2. I have pulled BMI and insurance charges values from the data set given. I make a table of values for these, but reduced the amount of data for easier calculations. Please use the data set (below) to answer the questions below.

\fStep 1: Choosing the Data You've chosen to analyze the average monthly temperatures in New York City over the past 20 years Thi value within a range). quas tive data (measured in degrees Fahrenheit) and continuous (temperature can take any Step 2: Observational or Experimental Study The data is from an observational study. The temperatures are recorded without any manipulation of variables. You are simply observing and recording data as it naturally occurs. Step 3: Interest in the Topic Interest in climate change and its impact on local weather patters. Analyzing the temperature data over a period of 20 years can provide insights into how climate change might be affecting New York City. Step 4: Collecting the Data Collected the average monthly temperatures for New York City over the past 20 years. Here is a subset of the raw data (one year as an example): 2010:[32.1, 352,420, 55.1, 65.3, 72.6, 77.5, 75.3, 68.0, 57.9, 47.2, 37.1] For simplicity, assume we have the complete dataset for all 20 years, giving us 240 data poi years x 12 months/year). Step 5: Histogram and Stem-and-Leaf Plot Using an online histogram calculator or software tool, we can plot the data. Histogram Frequency distribution for the temperature data Temperature Range (F) Frequency 3040 15 4050 3 s0-60 20 .70 s0 7060 w090 2 Histogram Title: Average Monthly Temperatures in New York City (2000-2020) Vertical Axis Label: Frequency Horizontal Axis Label: Temperature (F) Stem-and-Leaf Plot For simplicity, here's a stem-and-leaf plot for subset of the data: Stem Leaf. 3 2579 4 2468 5 02579 5 1358 7 025789 Step 6: Skew of the Data By examining the histogram, we can discuss the skewness of the data Symmetric: If the histogram is roughly symmetrical, the data is normally distributed. o Right Skew (Positively Skewed): If the histogram tails off to the right, the data is positively skewed, Left Skew (Negatively Skewed): I the histogram tails off to the left, the data is negatively skewed Step 7: Five-Number Summary The five-number summary includes the minimum, first quartile (Q1), median, third quartile (Q3), and maximum. Using the data: o Minimum (Min): 32.1F * First Quartile (Q1): 43.1F o Median: 57.9F o Third Quartile (Q3): 689F * Maximum (Max): 7.5 Step 8: Mean and Standard Deviation To calculate the mean and standard deviation, we use the following formulas: o Mean (s = & Standard Deviation (0): & Using a subset of data as an example: Sum of all data points (X): 14,000 Number of data points (N): 240 =140 = 58.33'F o=y X Step 9: Comparing Measures Compare the mean/standard deviation and five-number summary: Mean and Standard Deviation: Better if the data is normally distributed without outliers. o Five-Number Summary: Better if the data is skewed or contains outliers. Step 10: Summary Skewness The histogram shows if the data is right-skewed, indicating higher temperatures are more frequent. Outliers To check for outliers, use the IQR method: . IQRQ3 - Q1L o Lower bound: Q1 5% IQR Upper bound: Q3 + 1.5 x IQR For our example data: o IQR68.9 - 43.1 = 25.8 Lowerbound: 43.1 1.5 x 25.8 = 4.4 Upper bound: 68.9 + 1.5 x 25.8 = 107.6 Any data points outside this range are considered outliers. Summary 1. Skewness: The data might be right-skewed, indicating more frequent higher temperatures. 2. Outliers: Any data points below 44F or above 107.6F would be considered outliers. 3. Implications: The summary measures help us understand the central tendency and dispersion of temperatures, which is crucial for studying climate change trends. Conclusion The analysis of the average monthly temperatures in New York City over 20 years provides insights into local climate patterns. The skewness and outliers help us understand the distribution of temperatures, and the summary measures (mean, standard deviation, five-number summary) give a comprehensive overview of the data. This analysis can be extended to study the impact of climate change on local weather patterns. Let's go through the provided data and steps for Part 2 of the project in detail. Data Set for Analysis BMI Insurance Cost Per Year 27.50 1688492 4653 8686.39 2124 125721 3377 329018 1829 1036.78 25.41 237612 4192 913229 a. Independent and Dependent Variables o Independent Variable: BMI (predictor variable) o Dependent Variable: Insurance Cost Per Year (response variable) b. Linear Regression Model To create a linear regression model, we need to fit a line y = ma + b where y is the insurance cost and z is the BMI. Steps: . Calculate the mean of BMI (X) and the mean of Insurance Cost (). ~ . Calculate the slope m: S m= . Calculate the intercept b: b=Y -mX Calculations: 1. Mean Calculation: .77 + 18.: +25.41 + 41.92 - 27.90 + 46.53 + 21.24 + 3 = = g 20.46 v - 16884.92 + 8686.39 + 1257.21 + 3290.18 + 1036.78 + 2376.12 + 9132.29 7 6! . Sum of Products Calculation: X - X)(Y V) = (27.90 20.46)(16884.92 6566.53) + (46.53 29.46)(86 . Sum of Squares Calculation: Z(X X)? = (27.90 29.46)* + (46.53 29.46)* + ... = 696.57 . Slope Caleulation: . Intercept Calculation: b = 6566.53 (241.26 x 29.46) 6566.53 T114.71 548.18 So, the linear regression model is: Tnsurance Cost = 241.26 x BMI 548.18 c. Correlation Coefficient The correlation coefficient measures the strength and direction of a linear relationship between two variables. So, 167991.98 167991.98 V696.57 x 195276583.56 1r0zas 4 This indicates 2 moderate positive correlation between BMI and insurance cost. d. Scatterplot A sketch of the scatterplot with BMI on the x-axis and Insurance Cost on the y-axis would show a trend line representing the linear regression model. e. Outliers Using the scatterplot, any points that do not follow the overall trend can be considered outliers. For instance, the insurance cost for BMI 27.90 is much higher than expected, suggesting it could be an outlier. f. Predicting Insurance Cost for BMI of 17.21 Using the linear regression model: Insurance Cost = 241.26 x 17.21 548.18 Calculating: Insurance Cost = 4136.65 548.18 3588.47 g. Predicting BMI for Insurance Cost of $8000 Using the linear regression model: 8000 = 241.26 x BMI 548.18 Solving for BMI 8000 + 548.18 = 241.26 x BMI 8548.18 = 241.26 x BMI _ 854818 BMI = 35.43 h. Extrapolation Extrapolation occurs when making predictions outside the range of data, which can lead to unreliable resuits. Both parts f and g involve extrapolation. i. Trusting the Data Considering the data source (Kaggle dataset), the moderate correlation coefficient, and potential outliers, the data should be used with caution, especially when making predictions outside the observed range