Question
In a certain region, there is an average of 0.6 ant nests per square kilometre and an average of 0.3 beehives per square kilometre. Suppose
In a certain region, there is an average of 0.6 ant nests per square kilometre and an average of 0.3 beehives per square kilometre. Suppose that the locations of ant nests are independent of other ant nests, the locations of beehives are independent of other beehives, and the locations of ant nests and beehives are independent of each other.
a) Let A and B be the counts of ant nests and beehives, respectively, in a randomly chosen square kilometre. Justify why A follows a Poisson distribution with? = 0.6 and B follows a Poisson distribution with ? = 0.3.
b) Let S be the count of ant nests and beehives in a randomly chosen square kilometre. That is, let S = A + B. Use the moment generating function method to show that S follows a Poisson distribution with ? = 0.9.
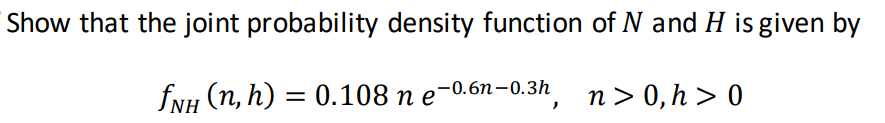
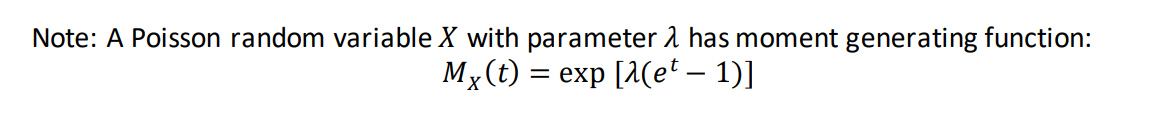
Step by Step Solution
There are 3 Steps involved in it
Step: 1

Get Instant Access to Expert-Tailored Solutions
See step-by-step solutions with expert insights and AI powered tools for academic success
Step: 2

Step: 3

Ace Your Homework with AI
Get the answers you need in no time with our AI-driven, step-by-step assistance
Get Started


