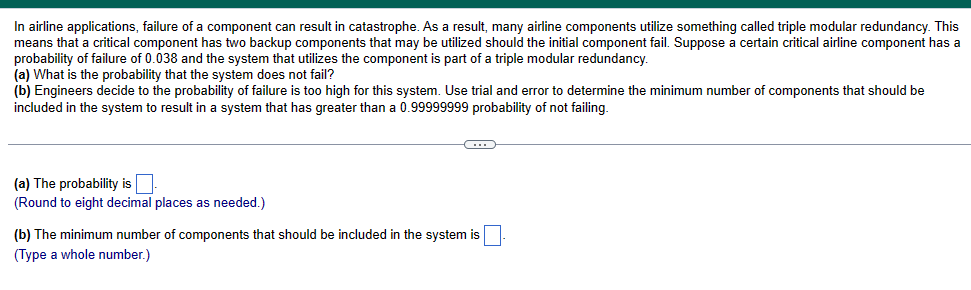
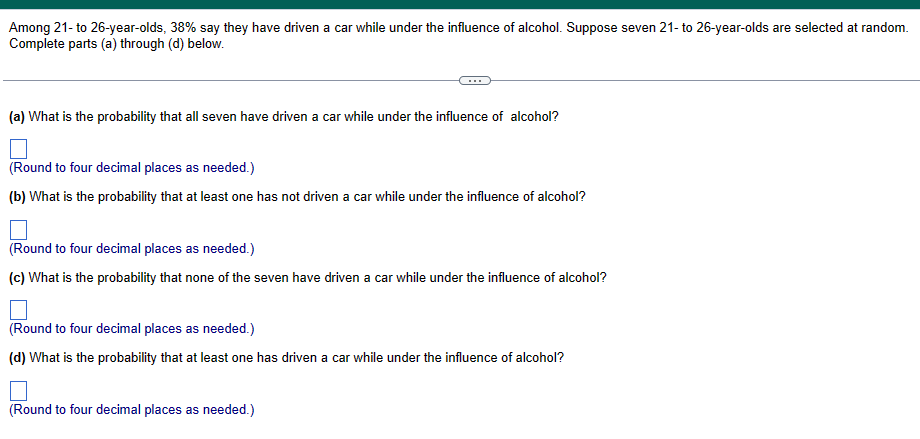
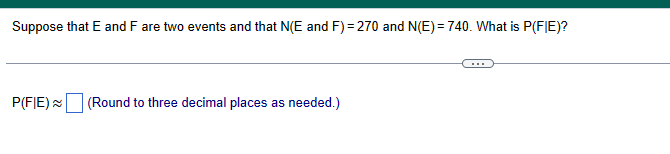
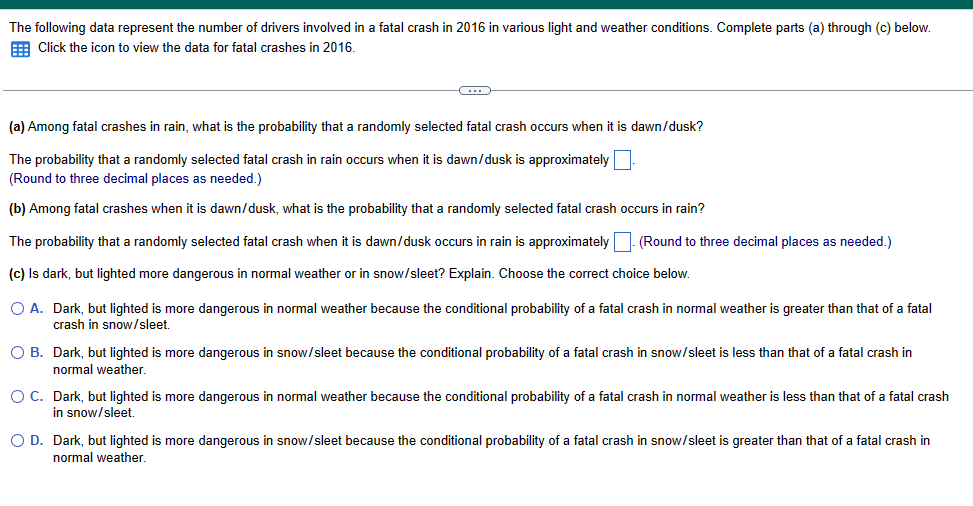
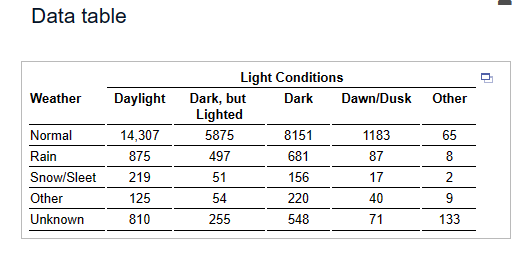
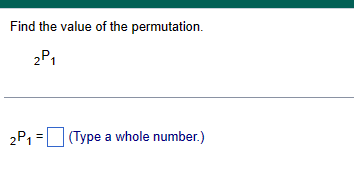
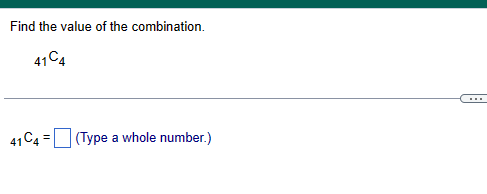
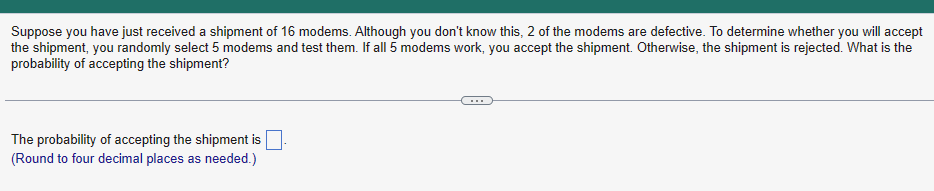
In airline applications, failure of a component can result in catastrophe. As a result, many airline components utilize something called triple modular redundancy. This means that a critical component has two backup components that may be utilized should the initial component fail. Suppose a certain critical airline component has a probability of failure of 0.038 and the system that utilizes the component is part of a triple modular redundancy. (a) What is the probability that the system does not fail? (b) Engineers decide to the probability of failure is too high for this system. Use trial and error to determine the minimum number of components that should be included in the system to result in a system that has greater than a 0.99999999 probability of not failing. (a) The probability is (Round to eight decimal places as needed.) (b) The minimum number of components that should be included in the system is (Type a whole number.) Among 21- to 26-year-olds, 38% say they have driven a car while under the influence of alcohol. Suppose seven 21- to 26-year-olds are selected at random. Complete parts (a) through (d) below. (a) What is the probability that all seven have driven a car while under the influence of alcohol? (Round to four decimal places as needed.) (b) What is the probability that at least one has not driven a car while under the influence of alcohol? (Round to four decimal places as needed.) (c) What is the probability that none of the seven have driven a car while under the influence of alcohol? (Round to four decimal places as needed.) (d) What is the probability that at least one has driven a car while under the influence of alcohol? (Round to four decimal places as needed.) Suppose that E and F are two events and that N(E and F) = 270 and N(E) = 740. What is P(FIE)? P(FIE) (Round to three decimal places as needed.) According to a recent study, 8.9% of high school dropouts are 16- to 17-year-olds. In addition, 5.6% of high school dropouts are white 16- to 17-year-olds. What is the probability that a randomly selected dropout is white, given that he or she is 16 to 17 years old? The probability that a randomly selected dropout is white, given that he or she is 16 to 17 years old, is (Round to four decimal places as needed.) The following data represent the number of drivers involved in a fatal crash in 2016 in various light and weather conditions. Complete parts (a) through (c) below. Click the icon to view the data for fatal crashes in 2016. (a) Among fatal crashes in rain, what is the probability that a randomly selected fatal crash occurs when it is dawn/dusk? The probability that a randomly selected fatal crash in rain occurs when it is dawn/dusk is approximately (Round to three decimal places as needed.) (b) Among fatal crashes when it is dawn/dusk, what is the probability that a randomly selected fatal crash occurs in rain? The probability that a randomly selected fatal crash when it is dawn/dusk occurs in rain is approximately . (Round to three decimal places as needed.) (c) Is dark, but lighted more dangerous in normal weather or in snow/sleet? Explain. Choose the correct choice below. A. Dark, but lighted is more dangerous in normal weather because the conditional probability of a fatal crash in normal weather is greater than that of a fatal crash in snow/sleet. B. Dark, but lighted is more dangerous in snow/sleet because the conditional probability of a fatal crash in snow/sleet is less than that of a fatal crash in normal weather. C. Dark, but lighted is more dangerous in normal weather because the conditional probability of a fatal crash in normal weather is less than that of a fatal crash in snow/sleet. D. Dark, but lighted is more dangerous in snow/sleet because the conditional probability of a fatal crash in snow/sleet is greater than that of a fatal crash in normal weather. Data table Light Conditions n Weather Daylight Dark, but Dark Dawn/Dusk Other Lighted Normal 14,307 5875 8151 1183 65 Rain 875 497 681 87 8 Snow/Sleet 219 51 156 17 2 Other 125 54 220 40 9 Unknown 810 255 548 71 133 The data on the right represent the number of traffic fatalities by seat location and gender. Determine P(male) and P(male|driver). Are the events "male" and "driver" independent? Female Male Total P Driver 32,980 11,914 44,894 Passenger 6,453 6,201 12,654 Total 39,433 18,115 57,548 Determine P(male). P(male) = (Round to three decimal places as needed.) Determine P(male|driver). P(male|driver) = (Round to three decimal places as needed.) Are the events "male" and "driver" independent? A. No. The occurrence of the event "driver" affects the probability of the event "male." B. Yes. The occurrence of the event "driver" affects the probability of the event "driver." C. No. The occurrence of the event "driver" does not affect the probability of the event "male." D. Yes. The occurrence of the event "driver" does not affect the probability of the event "male." Find the value of the permutation. 2P1 2P1 = (Type a whole number.) Find the value of the combination. 41C4 41C4 = (Type a whole number.) Companies whose stocks are listed in a stock exchange have their company name represented by either one, three, or four letters (repetition of letters is allowed). What is the maximum number of companies that can be listed on the stock exchange? The maximum number of companies that can be listed on the stock exchange is (Type a whole number.) A golf-course architect has four linden trees, five white birch trees, and three bald cypress trees to plant in a row along a fairway. In how many ways can the landscaper plant the trees in a row, assuming that the trees are evenly spaced? The trees can be planted in different ways. Suppose you have just received a shipment of 16 modems. Although you don't know this, 2 of the modems are defective. To determine whether you will accept the shipment, you randomly select 5 modems and test them. If all 5 modems work, you accept the shipment. Otherwise, the shipment is rejected. What is the probability of accepting the shipment? The probability of accepting the shipment is (Round to four decimal places as needed.)