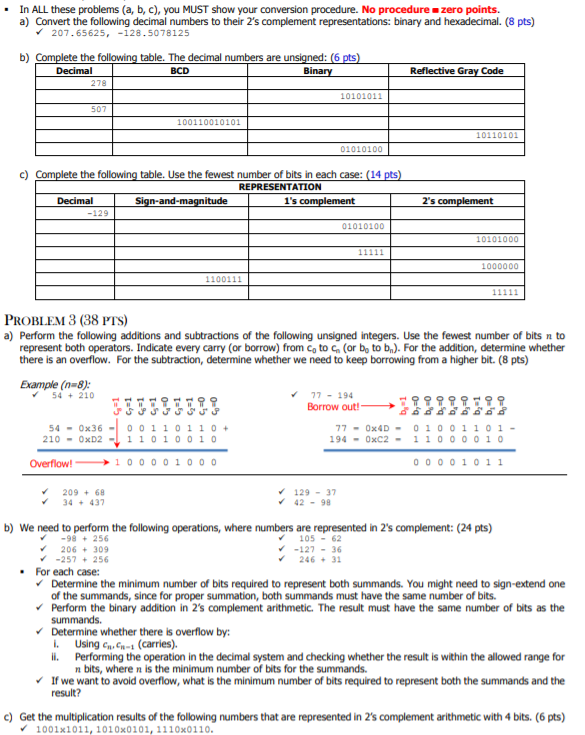
. In ALL these problems (a, b, c), you MUST show your conversion procedure. No procedure = zero points. a) Convert the following decimal numbers to their 2's complement representations: binary and hexadecimal. (8 pts) 207.65625, -128.5078125 b) Complete the following table. The decimal numbers are unsigned: (6 pts) Decimal Binary Reflective Gray Code BCD 278 10101011 507 100110010101 10110101 01010100 c) Complete the following table. Use the fewest number of bits in each case: (14 pts) REPRESENTATION Decimal Sign-and-magnitude 1's complement -129 01010100 2's complement 10101000 11111 1000000 1100111 11111 PROBLEM 3 (38 PTS) a) Perform the following additions and subtractions of the following unsigned integers. Use the fewest number of bits n to represent both operators. Indicate every carry (or borrow) from C, to (or bo to b.). For the addition, determine whether there is an overflow. For the subtraction, determine whether we need to keep borrowing from a higher bit. (8 pts) Example (n=8): 54 + 210 77 - 194 Borrow out! 54 - 0x36 - 001101 77 - OxD - 01001101 - 210 - 0xD2 -11010010 194 - 0xC2 - 11000010 Overflow! 10000 1000 00001011 0 - 0+ 209 + 69 34 + 437 129 - 37 42 - 99 b) We need to perform the following operations, where numbers are represented in 2's complement: (24 pts) -98 + 256 105 - 62 206 + 309 -127 - 36 -257 + 256 246 + 31 . For each case: Determine the minimum number of bits required to represent both summands. You might need to sign-extend one of the summands, since for proper summation, both summands must have the same number of bits. Perform the binary addition in 2's complement arithmetic. The result must have the same number of bits as the summands. Determine whether there is overflow by: 1. Using CC (carries). II. Performing the operation in the decimal system and checking whether the result is within the allowed range for n bits, where n is the minimum number of bits for the summands. If we want to avoid overflow, what is the minimum number of bits required to represent both the summands and the result? c) Get the multiplication results of the following numbers that are represented in 2's complement arithmetic with 4 bits. (6 pts) 1001x1011, 10100101, 11100110. . In ALL these problems (a, b, c), you MUST show your conversion procedure. No procedure = zero points. a) Convert the following decimal numbers to their 2's complement representations: binary and hexadecimal. (8 pts) 207.65625, -128.5078125 b) Complete the following table. The decimal numbers are unsigned: (6 pts) Decimal Binary Reflective Gray Code BCD 278 10101011 507 100110010101 10110101 01010100 c) Complete the following table. Use the fewest number of bits in each case: (14 pts) REPRESENTATION Decimal Sign-and-magnitude 1's complement -129 01010100 2's complement 10101000 11111 1000000 1100111 11111 PROBLEM 3 (38 PTS) a) Perform the following additions and subtractions of the following unsigned integers. Use the fewest number of bits n to represent both operators. Indicate every carry (or borrow) from C, to (or bo to b.). For the addition, determine whether there is an overflow. For the subtraction, determine whether we need to keep borrowing from a higher bit. (8 pts) Example (n=8): 54 + 210 77 - 194 Borrow out! 54 - 0x36 - 001101 77 - OxD - 01001101 - 210 - 0xD2 -11010010 194 - 0xC2 - 11000010 Overflow! 10000 1000 00001011 0 - 0+ 209 + 69 34 + 437 129 - 37 42 - 99 b) We need to perform the following operations, where numbers are represented in 2's complement: (24 pts) -98 + 256 105 - 62 206 + 309 -127 - 36 -257 + 256 246 + 31 . For each case: Determine the minimum number of bits required to represent both summands. You might need to sign-extend one of the summands, since for proper summation, both summands must have the same number of bits. Perform the binary addition in 2's complement arithmetic. The result must have the same number of bits as the summands. Determine whether there is overflow by: 1. Using CC (carries). II. Performing the operation in the decimal system and checking whether the result is within the allowed range for n bits, where n is the minimum number of bits for the summands. If we want to avoid overflow, what is the minimum number of bits required to represent both the summands and the result? c) Get the multiplication results of the following numbers that are represented in 2's complement arithmetic with 4 bits. (6 pts) 1001x1011, 10100101, 11100110
