*** IN C LANGUAGE ***

When you were younger, you were informed that you could not simultaneously have and eat your cake. You being of sound mind (and of decent programming skill) have decided to disprove such an assertion.

You have a circular cake with a specified radius, and you plan on cutting it exactly once (on a vertical line) such that the ratio of the area of the left portion to the area of the right portion is a specific value. You will eat the left portion, and the right portion you will have.

Problem

Given the description of a circular cake and a desired ratio of eaten cake to non-eaten cake you must find a line in the form of x = a, such that the area of cake to the left of the line and the area of cake to the right of line meets the desired ratio.

Input Specification

The first and only line of input will have 3 positive integers, each less than 10,000. The first value, r, represents the radius of the cake. The second and third value, L and R, represent the ratio of left area to right area desired.

Output Specification

For the cake simply output the x coordinate of the vertical cut that splits the cake into the areas that have the ratio L to R. Assume that the center of the cake is at point (0,0) in the Cartesian plane. Answers that are within absolute or relative error of at most 10^-6 of the solution will be accepted (e.g. if the answer is .5, then .4999990 is close enough, but .4999989 is not).

Input Output Example

Explanation

Case 1:

Pictorially the resulting cut looks like the following.

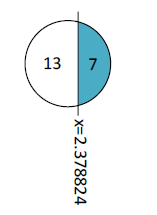
The blue area is 7/13 of the white area of the circle

Case 2:

Pictorially the resulting cut looks like the following.

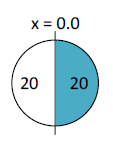
The areas of the two sections are equal

Case 3:

Pictorially the resulting cut looks like the following:

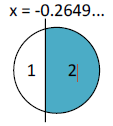
Supplemental Information (Geometry Spoilers) The area of the blue section is twice the area of the white section.

For those of you who dont have the strongest geometry/trigonometry background lets cover a few geometric properties that can assist you with the math.

First lets talk about the area of a triangle. Many of you know the one half base times height formula, but without knowledge of the exact height what can be done. Suppose we know two side lengths and the angle between them. We can treat one length as the base of the triangle and the height should be perpendicular to the base. With this information we can make a height by using some trigonometric properties of right triangles. See the example the line c is formed from the right triangle with b as the hypotenuse. The length of c must be b times the sin of the angle between a and b. Since c is perpendicular to a. The height of the triangle with a as the base is c.

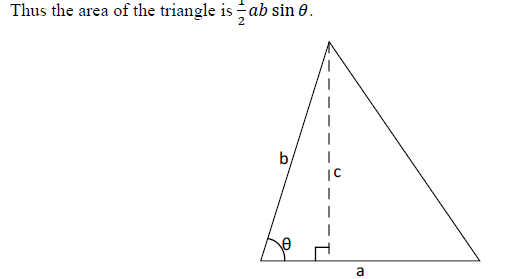
The next part that is very important is related to finding parts of the area of a circle. Suppose we wanted to know the area of a slice of a pizza, but we only know the radius and the number of slice (which should be equal in size). This make finding the area very easy. We could find the area using the standard formula (one half pi radius squared) and divide by the number of slices. For the below example the area is one eighth the original area.

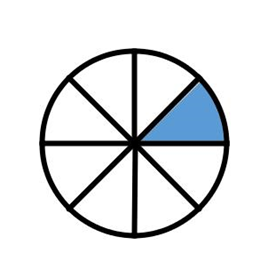
Suppose we want to know the area of multiple slices, assuming they are of equal size we could multiply the area of one slice by the number of slices we need to consider. The area below is three times one eighth the original area (or three eighths the original area).

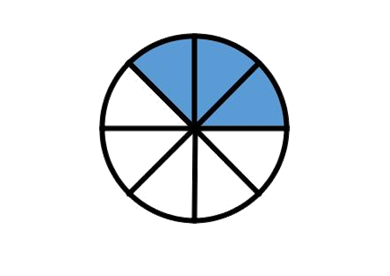
Following this lets consider a situation in which each slices angle is exactly one degree. To find the area of a circular sector with angle equal to some integral degree q what would we do? We could find the area of the circular sector that comprises of only one degree which we can think of as our slices area (this means the slices area is one 360^th of the original circles area or pi times the radius squared over 360). Then multiply by the number of slices we need, which happens to be q. In other words the sectors area is q times pi times radius squared over 360.

As it so happens this works for non-integral q as well (i.e. if q is one half, then the slices area is one half the area of a circular sector whose angle is 1 degree).

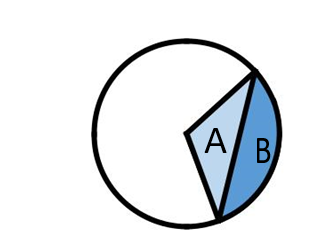
The last thing that can help you with this project is try to consider the area of a circular sector as the addition of two different areas. One is a triangle the other is the area of a circular segment. In the following example the circular segment (B) is the circular sector (A+B) minus the triangle (A),

Math.h

A source file you might find quite useful is . To use it put at the top of your code (in your includes) the line #include . A few useful functions that come with math.h include,

- sqrt(x) which finds the square root of the given parameter x,

- sin(x)/cos(x) which return the sine/cosine of an angle x in radians,

- asin(x)/acos(x) which returns in radians the arc sine/arc cosine of a value x ? [0.0, 1.0].

Grading Information

Reading from standard input 5 points

Writing to standard output 5 points

Comments, white space usage, and reasonable variable names 10 points

No output aside from the answer (e.g. no input prompts) 10 points.

Attempts to find the area of a circular segment 10 points

Uses 10 points

Your program will be tested on 10 test cases 5 points each

No points will be awarded to programs that do not compile.

Solutions without binary search will receive a maximum of 50 points

Only cases that finish within the maximum of {5 times the judge solution, 10 seconds} will be graded.

Input 10 13 7 2.3788243932 5 20 200.0000000000 11 2 Output 0.2649320846 Input 10 13 7 2.3788243932 5 20 200.0000000000 11 2 Output 0.2649320846