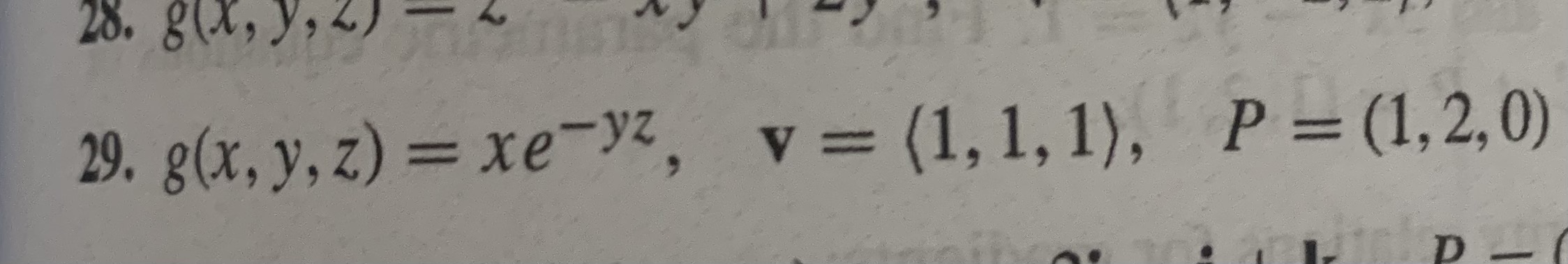In Exercises 21-30, calculate the directional derivative in the direction of v at the given point. Remember to use a unit vector in your directional derivative computation.28. 8( X, ), 4 ) -4 29. g (x, y, z) = xe-yz V = (1, 1, 1), P = (1, 2, 0) D38. Calculate az/ax and az/ay at the points (3, 2, 1) and (3, 2, -1), where BRAINS SECTION 15.6 A Multivariable Calculus Chain Rules 855 : is defined implicitly by the equation z* + z2x2 - y - 8 =0. In Exercises 29-34, calculate the partial derivative using implicit differ- entiation. 12 2y + 12z + x22 = 10 " ar' ( To ) dw x2w+ w' + wz + 3 yz= 0 30. -' z =-4 e" + sin(xz) +y=0 31. av at - and a 12 = teslr 12. jesh words of siull routof hadfuntuga FIGURE 9 Graph of x2 + y2 - z2 - 12x - 8z - 4 =0. 33. ow W 2 + x 2 w 2 + 1 2 2 = 1 at (x, y, w) = (1, 1, 1) 40. For all x > 0, there is a unique value y = r(x) that solves the equation y3 + 4xy = 16. 34. au/aT and aT/aU, (TU - V)2 In(W - UV) = In2 at (a) Show that dy / dx = -4y/(3y2 + 4x). (7,U, V, W) = (1, 1, 2, 4) (b) Let g(x) = f(x, r(x)), where f(x, y) is a function satisfying fx ( 1, 2 ) = 8, fy (1, 2) = 10 35. Letr = (x, y, z) and er = r/Irl|. Show that if a function f (x, y, z) = F(r) depends only on the distance from the origin r = Irl| = Use the Chain Rule to calculate g'(1). Note that r(1) = 2 because (x, y) = Viz + yz + z2, then (1, 2) satisfies y' + 4xy = 16. 41. The pressure P, volume V, and temperature T of a van der Waals gas Vf = F'(r)er 9 with n molecules (n constant) are related by the equation (P + 12 ) ( V - nb ) = nRT 36. Let f (x, y, z) = e-x2-12-22 = e-12 , with r as in Exercise 35. Com- pute Vf directly and using Eq. (9). where a, b, and R are constant. Calculate a P /aT and aV /aP. 37. Use Eq. (9) to compute V (). 42. When x, y, and z are related by an equation F(x, y, z) = 0, we some- times write (Oz/ax)y in place of az/ax to indicate that in the differentia- tion, z is treated as a function of x with y held constant (and similarly for 38. Use Eq. (9) to compute V(Inr).( 5) Job rogo pe prize the other variables). (a) Use Eq. (7) to prove the cyclic relation 39. Figure 9 shows the graph of the equation s solv muniz (ay ) =-1 10 F (x, y, z) = x2 + 32 - 22 - 12x -82-4=0 (b) Verify Eq. (10) for F(x, y, z) = x ty + z=0. (a) Use the quadratic formula to solve for z as a function of x and y. This (c) Verify the cyclic relation for the variables P, V, T in the Ideal Gas gives two formulas, depending on the choice of sign. ohLaw PV - nRT = 0 (n and R are constants). (b) Which formula defines the portion of the surface satisfying z 2 -4? Blue 43. Show that if f(x) is differentiable and c # 0 is a constant, then Which formula defines the portion satisfying z - -4? reun u(x, t) = f(x - ct) satisfies the so-called advection equation (c) Calculate az/ax using the formula z = f(x, y) (for both choices of apis du du sign) and again via implicit differentiation. Verify that the two answers = 0 agree. legree n, then fx (x, y, z)