In international security, the value of alliances depends on the reliability of the allies that form them. The anticipation that a reliable ally will defend a target of aggression may lead an attacker to anticipate punishment. Anticipating punishment, the attacker will not attack. The alliance game in Figure 1 attempts to model this reasoning. A challenger (Nation A) has the choice to attack a target (Nation B) or not to attack it and its optimal action hinges on its beliefs about the targets ally (Nation C). Crucially, the ally may be reliable or unreliable and only the ally knows if it is reliable; the challenger is not sure. If the ally is (perceived to be) reliable, then the challenger will not attack, while if the ally is (perceived to be) unreliable, the challenger will attack. If the challenger attacks and it is right in the estimate of the allys reliability, then the ally will stay out. In Figure 1, there are three players: Country A, the potential attacker; country B, the potential target; and country C, the potential ally of country B. For each outcome, As payoff is listed first, Bs payoff is listed second, and Cs payoff is listed third. Preferences are ordered so that a is the most preferred outcome, while d is the worst. That is, a > b > c > d. C might be one of two types of allies, a reliable or an unreliable ally. The top subgame of the tree represents an ally C that is reliable. Given the move by nature, there is a probability p that the attacker is facing a target with a reliable ally. The lower subgame of the tree represents an ally C that is unreliable. Given the move by nature, there is a probability 1 p that the attacker is facing a target with an unreliable ally. The potential outcomes of the game are the Status Quo, A Wins, a war where B Fights Alone, and a war where B and C Join against A. First, solve each part of the game as if there were no uncertainty. Write out the preference orderings for the players. The payoffs are actually already written in the game tree in Figure 1 . For reference, write them out here in summary form. For example, working from the game we can see that As preferences are A Wins B Fights Alone Status Quo War against B and C

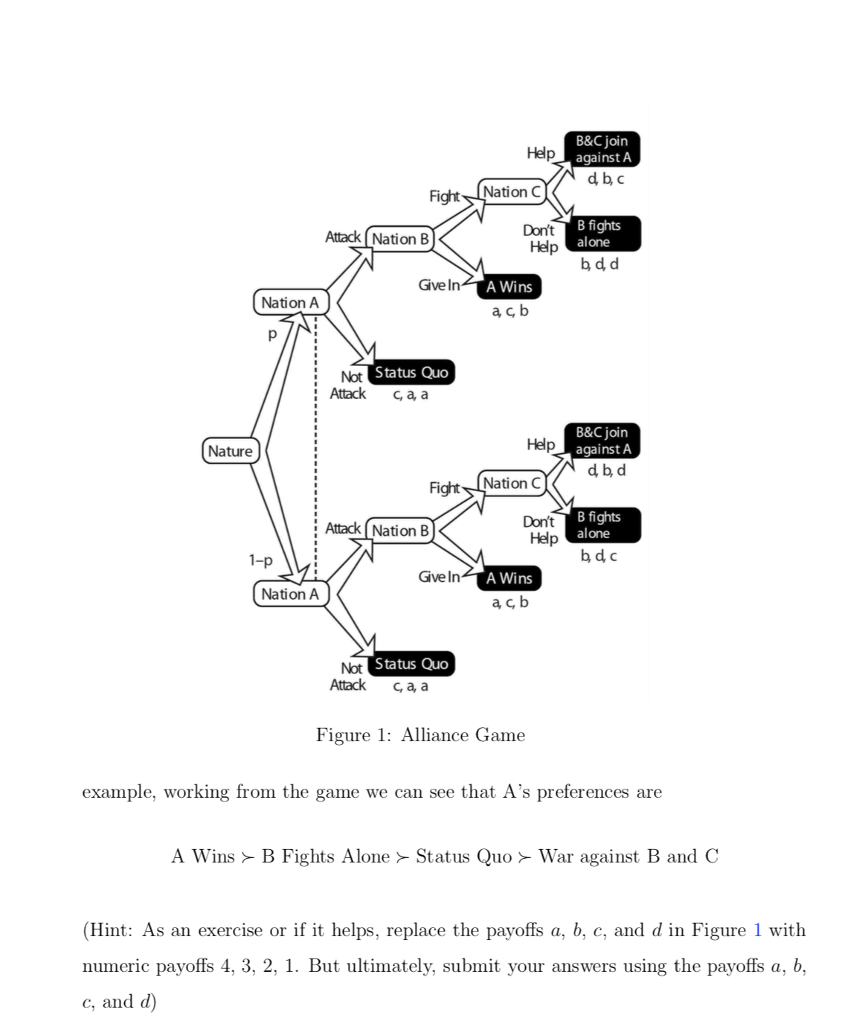
(e) Next, solve for the critical value of probability p. Because the outcome in the two subtrees is different, what the challenger does is dependent on the challengers beliefs about the allys type. Compute the expected utility to Country A from attacking. Write out Country As EUA(attack) and simplify the expression as much as you can (1 point). (f) Compute the expected utility to Country A from not attacking. Write out Coun- try As EUA(do not attack) and simplify the expression as much as you can (1 point). (g) To attack, the payoff from the attack to Country A must be greater than the payoff from the status quo (not attacking). Solve for the critical value of p that makes this true and state the inequality that summarizes when attacking is preferred to not attacking. (Hint: the result in this case will not be a number but an expression involving payoffs a, b, c, and/or d.) (3 points)

B&C join Help against A db, Fight Nation Attack (Nation B Don't B fights Help alone bd d Give In A Wins Nation A acb p Not Status Quo Attack , Nature Attack (Nation B B&C join Help against A dbd Fight Nation C Don't B fights Help alone bdc Give In A Wins acb 1-p Nation A Not Status Quo Attack ca, a Figure 1: Alliance Game example, working from the game we can see that A's preferences are A Wins > B Fights Alone Status Quo > War against B and C (Hint: As an exercise or if it helps, replace the payoffs a, b, c, and d in Figure 1 with numeric payoffs 4, 3, 2, 1. But ultimately, submit your answers using the payoffs a, b, c, and d) B&C join Help against A db, Fight Nation Attack (Nation B Don't B fights Help alone bd d Give In A Wins Nation A acb p Not Status Quo Attack , Nature Attack (Nation B B&C join Help against A dbd Fight Nation C Don't B fights Help alone bdc Give In A Wins acb 1-p Nation A Not Status Quo Attack ca, a Figure 1: Alliance Game example, working from the game we can see that A's preferences are A Wins > B Fights Alone Status Quo > War against B and C (Hint: As an exercise or if it helps, replace the payoffs a, b, c, and d in Figure 1 with numeric payoffs 4, 3, 2, 1. But ultimately, submit your answers using the payoffs a, b, c, and d)