In January 2011, a Bahraini girl wanted her younger brother to see snow. Panasonics SPARKS team answered the call by shipping a snowman from Japan (5314 miles over 40 hours of Journey) without refrigeration. They accomplished it by using U-Vacua, an insulation material that is many better than our usual home insulation. To understand how this feat was accomplished, the package can be simplified as concentric spheres.

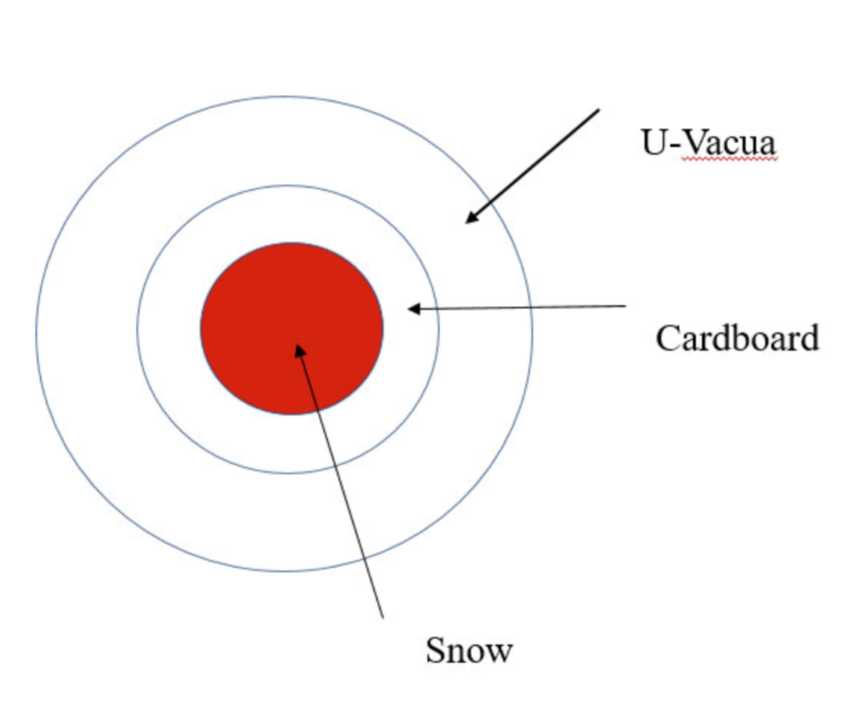
Assume heat transfer is at steady-state. The thermal conductivities of the cardboard and U-Vacua are 0.067 and 0.0007 W/m-K respectively. The radius of snow, carboard, and U-Vacua are 50, 60, and 62 cm respectively. At the snow-cardboard interface, the temperature is at 0 0C. The outside air temperature is at 43 0C and the convective heat transfer coefficient is 10 W/m2-K.

(a) Write down the governing equation and boundary conditions for the problem. NOTE: you will have one GE for each component.

(b) What are the boundary conditions needed to solve this problem?

(c) Derive an equation for the conductive thermal resistance of the composite shown above.

(d) Calculate the rate of heat gained from the ambient air to the snow.

(e) Calculate the temperature at the interface of cardboard and U-Vacua

(f) The latent heat of fusion is 333 J/kg, and the density of snow is 700 kg/m3. What is the heat gained over the 40-hour period, and what fraction of the snow will melt, assuming that the snow is always at 00C?

U-Vacua Cardboard Snow