In Java please


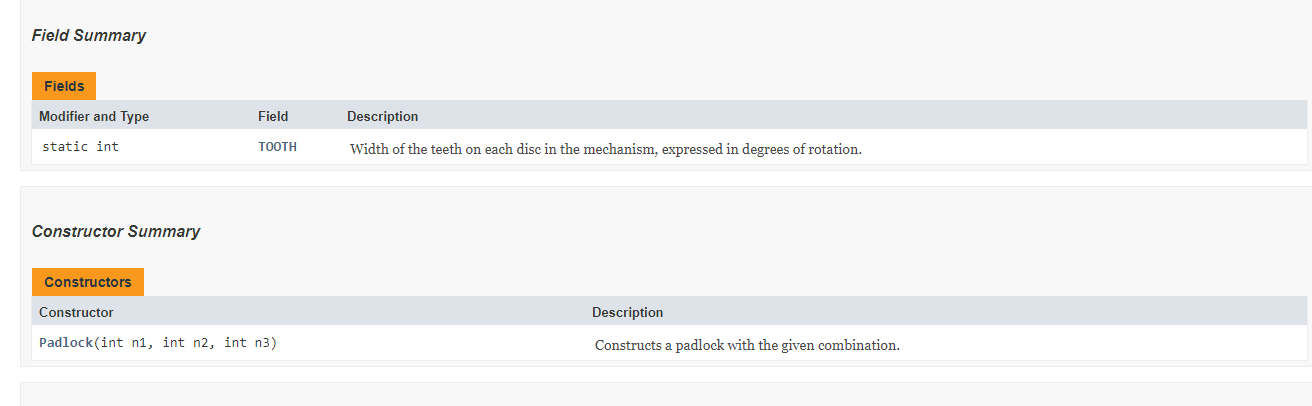
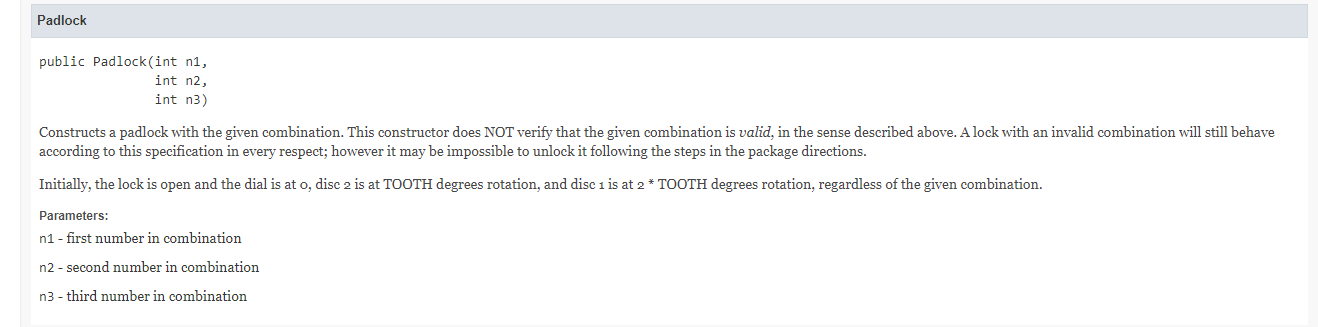
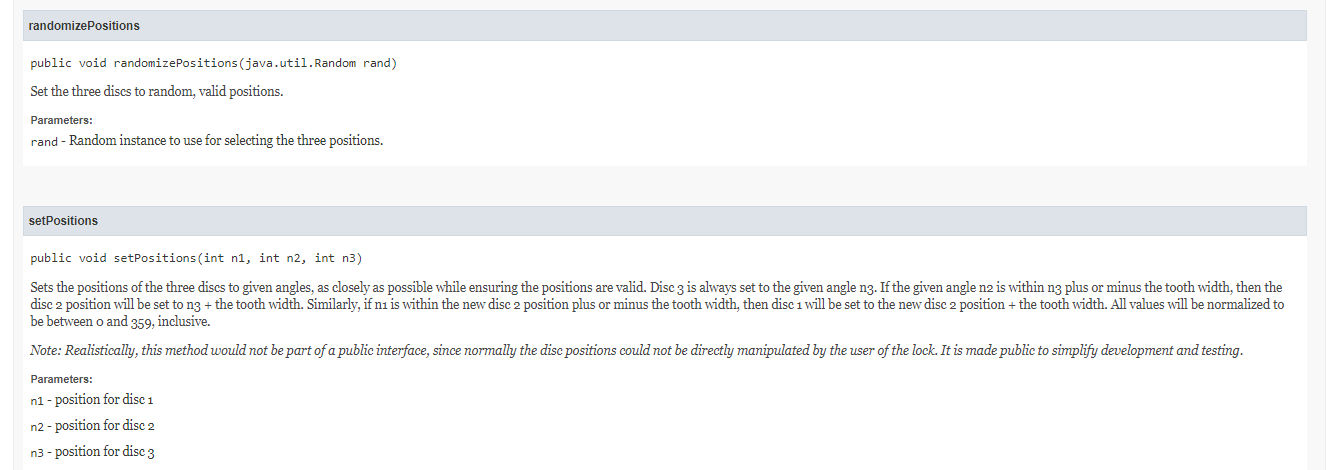
We describe the position of each disc as the number of degrees that its tooth is rotated counterclockwise from the zero position at the top. In general, we require this number to be "normalized" so it is in the range from o through 359. For the front disc, its position always matches the number at the top of the dial; i.e., we assume the tooth is at the number o. Each disc also has an offset, in degrees, between its tooth and the notch. If the notch is in the correct alignment position when the disc's position is D degrees, then we say the offset is D. When every dise's current position is equal to its offset, then the notches are aligned and the lock can be opened. It is the amount of these offsets that determine the combination. The way we interpret a combination X, Y, Z is like this: rotate the dial two complete revolutions clockwise and stop at X rotate the dial one complete revolution counterclockwise and stop at Y rotate the dial clockwise and stop at Z It would be convenient if when the combination is X, Y, Z the offsetsfor discs 1, 2, and 3 respectively, would simply be X, Y, Z. However, if we turn the dial several complete revolutions counterclockwise and stop when the dial is at, say, 100 degrees, the other two discs will not be rotated 100 degrees. We also have to account for the width of the tooth itself. If, for example, the tooth is wide enough to occupy two degrees worth of the disc's rotation, then in this scenario our disc 2 would be at 102 degrees and disc 1 would be at 104 degrees. Similarly, if we rotate the dial clockwise a full revolution and stop at 100 degrees, the middle disc would be at 98. In general to get combination X, Y, Z, the offsets would be X-2* TOOTH for disc 1, Y + TOOTH for disc 2, and Z for disc 3, where TOOTH is the width of the tooth expressed in degrees. Note we are assuming that both of the teeth for disc 2 are in the same position. The constructor arguments consist of three numbers that represent the intended combination, from which the offsets can be calculated as above and then normalized). Not every set of three numbers is a valid combination, i.e., one that could actually be used to open a lock, but the constructor will NOT verify that the three given numbers are valid. If the constructor arguments don't form a valid combination, the resulting lock will simply be unable to be opened because for one reason or another it is impossible for the discs to become correctly aligned. In every other respect a lock with an invalid combination will behave according to this specification. For the sake of general interest, and in order to construct valid test cases, here is a high-level description of what makes a valid combination. There are two sets of requirements. Given combination ni, n2, n3, let 01 = n1 - 2 * TOOTH, 02 = n2 + TOOTH, and 03 = n3 be the corresponding offsets. For the sake of general interest, and in order to construct valid test cases, here is a high-level description of what makes a valid combination. There are two sets of requirements. Given combination ni, n2, n3, let 01 = n1 - 2* TOOTH, 02 = n2 + TOOTH, and 03 = n3 be the corresponding offsets. First, the offsets themselves have to be valid. That just means that the teeth don't overlap; that is, the 01 is rotated at least plus or minus TOOTH from 02, and o2 is rotated at least plus or minus TOOTH from 03. Second, the offsets have to be feasible. That means you can actually get the discs into those positions by entering the combination according to the package directions. This additional restriction is due to the fact that the second step in the combination is to turn counterclockwise a full rotation, and then continue turning counterclockwise until disc 2 reaches its offset position. However, this second rotation is not supposed to move disc 1 again. Therefore, the minimum counterclockwise angle between o1 and o2 is 2 * TOOTH (where disk 2 ends up after the full counterclockwise rotation) and the maximum counterclockwise angle is 360 - 2* TOOTH (after which disc 1 would get pushed counterclockwise). Example: Assume a TOOTH width of 2. Combination 4, 0, 4 would have offsets 0, 2, 4. This is invalid since the rotation from 01 to 02 is only two degrees. Picture what happens when you turn two revolutions clockwise and stop at 4. That leaves disc 1 at position o, as required. Then rotate 360 degrees counterclockwise, leaving disc 3 at position 4 and disc 2 at position 6. You can continue pushing disc 2 counterclockwise to any position from 6 through 358, but if you go any farther it will cause disc 1 to move again, so you can't turn the dial past 356. Example: Combination 4, 4, 4 is valid. The offsets would be o, 6, 4. Once you do the two clockwise revolutions and then stop at 4, disc 1 is at position o. Then a full counterclockwise rotation leaves disc 2 at position 6. Then disc 3 is already at position 4, so turning it clockwise zero degrees leaves it at position 4, and we have the correct alignment. Field Summary Fields Modifier and Type Field Description static int TOOTH Width of the teeth on each disc in the mechanism, expressed in degrees of rotation. Constructor Summary Constructors Constructor Description Padlock(int ni, int n2, int n3) Constructs a padlock with the given combination. Padlock public Padlock(int n1, int n2, int n3) Constructs a padlock with the given combination. This constructor does NOT verify that the given combination is valid, in the sense described above. A lock with an invalid combination will still behave according to this specification in every respect; however it may be impossible to unlock it following the steps in the package directions. Initially, the lock is open and the dial is at o, disc 2 is at TOOTH degrees rotation, and disc 1 is at 2 * TOOTH degrees rotation, regardless of the given combination. Parameters: n1 - first number in combination n2 - second number in combination n3 - third number in combination randomizePositions public void randomizePositions (java.util. Random rand) Set the three discs to random, valid positions. Parameters: rand - Random instance to use for selecting the three positions. setPositions public void setPositions(int ni, int n2, int n3) Sets the positions of the three discs to given angles, as closely as possible while ensuring the positions are valid. Disc 3 is always set to the given angle n3. If the given angle ne is within ng plus or minus the tooth width, then the disc 2 position will be set to n3 + the tooth width. Similarly, if ni is within the new disc 2 position plus or minus the tooth width, then disc 1 will be set to the new disc 2 position + the tooth width. All values will be normalized to be between o and 359, inclusive. Note: Realistically, this method would not be part of a public interface, since normally the disc positions could not be directly manipulated by the user of the lock. It is made public to simplify development and testing. Parameters: nl - position for disc 1 n2-position for disc 2 n3 - position for disc 3 We describe the position of each disc as the number of degrees that its tooth is rotated counterclockwise from the zero position at the top. In general, we require this number to be "normalized" so it is in the range from o through 359. For the front disc, its position always matches the number at the top of the dial; i.e., we assume the tooth is at the number o. Each disc also has an offset, in degrees, between its tooth and the notch. If the notch is in the correct alignment position when the disc's position is D degrees, then we say the offset is D. When every dise's current position is equal to its offset, then the notches are aligned and the lock can be opened. It is the amount of these offsets that determine the combination. The way we interpret a combination X, Y, Z is like this: rotate the dial two complete revolutions clockwise and stop at X rotate the dial one complete revolution counterclockwise and stop at Y rotate the dial clockwise and stop at Z It would be convenient if when the combination is X, Y, Z the offsetsfor discs 1, 2, and 3 respectively, would simply be X, Y, Z. However, if we turn the dial several complete revolutions counterclockwise and stop when the dial is at, say, 100 degrees, the other two discs will not be rotated 100 degrees. We also have to account for the width of the tooth itself. If, for example, the tooth is wide enough to occupy two degrees worth of the disc's rotation, then in this scenario our disc 2 would be at 102 degrees and disc 1 would be at 104 degrees. Similarly, if we rotate the dial clockwise a full revolution and stop at 100 degrees, the middle disc would be at 98. In general to get combination X, Y, Z, the offsets would be X-2* TOOTH for disc 1, Y + TOOTH for disc 2, and Z for disc 3, where TOOTH is the width of the tooth expressed in degrees. Note we are assuming that both of the teeth for disc 2 are in the same position. The constructor arguments consist of three numbers that represent the intended combination, from which the offsets can be calculated as above and then normalized). Not every set of three numbers is a valid combination, i.e., one that could actually be used to open a lock, but the constructor will NOT verify that the three given numbers are valid. If the constructor arguments don't form a valid combination, the resulting lock will simply be unable to be opened because for one reason or another it is impossible for the discs to become correctly aligned. In every other respect a lock with an invalid combination will behave according to this specification. For the sake of general interest, and in order to construct valid test cases, here is a high-level description of what makes a valid combination. There are two sets of requirements. Given combination ni, n2, n3, let 01 = n1 - 2 * TOOTH, 02 = n2 + TOOTH, and 03 = n3 be the corresponding offsets. For the sake of general interest, and in order to construct valid test cases, here is a high-level description of what makes a valid combination. There are two sets of requirements. Given combination ni, n2, n3, let 01 = n1 - 2* TOOTH, 02 = n2 + TOOTH, and 03 = n3 be the corresponding offsets. First, the offsets themselves have to be valid. That just means that the teeth don't overlap; that is, the 01 is rotated at least plus or minus TOOTH from 02, and o2 is rotated at least plus or minus TOOTH from 03. Second, the offsets have to be feasible. That means you can actually get the discs into those positions by entering the combination according to the package directions. This additional restriction is due to the fact that the second step in the combination is to turn counterclockwise a full rotation, and then continue turning counterclockwise until disc 2 reaches its offset position. However, this second rotation is not supposed to move disc 1 again. Therefore, the minimum counterclockwise angle between o1 and o2 is 2 * TOOTH (where disk 2 ends up after the full counterclockwise rotation) and the maximum counterclockwise angle is 360 - 2* TOOTH (after which disc 1 would get pushed counterclockwise). Example: Assume a TOOTH width of 2. Combination 4, 0, 4 would have offsets 0, 2, 4. This is invalid since the rotation from 01 to 02 is only two degrees. Picture what happens when you turn two revolutions clockwise and stop at 4. That leaves disc 1 at position o, as required. Then rotate 360 degrees counterclockwise, leaving disc 3 at position 4 and disc 2 at position 6. You can continue pushing disc 2 counterclockwise to any position from 6 through 358, but if you go any farther it will cause disc 1 to move again, so you can't turn the dial past 356. Example: Combination 4, 4, 4 is valid. The offsets would be o, 6, 4. Once you do the two clockwise revolutions and then stop at 4, disc 1 is at position o. Then a full counterclockwise rotation leaves disc 2 at position 6. Then disc 3 is already at position 4, so turning it clockwise zero degrees leaves it at position 4, and we have the correct alignment. Field Summary Fields Modifier and Type Field Description static int TOOTH Width of the teeth on each disc in the mechanism, expressed in degrees of rotation. Constructor Summary Constructors Constructor Description Padlock(int ni, int n2, int n3) Constructs a padlock with the given combination. Padlock public Padlock(int n1, int n2, int n3) Constructs a padlock with the given combination. This constructor does NOT verify that the given combination is valid, in the sense described above. A lock with an invalid combination will still behave according to this specification in every respect; however it may be impossible to unlock it following the steps in the package directions. Initially, the lock is open and the dial is at o, disc 2 is at TOOTH degrees rotation, and disc 1 is at 2 * TOOTH degrees rotation, regardless of the given combination. Parameters: n1 - first number in combination n2 - second number in combination n3 - third number in combination randomizePositions public void randomizePositions (java.util. Random rand) Set the three discs to random, valid positions. Parameters: rand - Random instance to use for selecting the three positions. setPositions public void setPositions(int ni, int n2, int n3) Sets the positions of the three discs to given angles, as closely as possible while ensuring the positions are valid. Disc 3 is always set to the given angle n3. If the given angle ne is within ng plus or minus the tooth width, then the disc 2 position will be set to n3 + the tooth width. Similarly, if ni is within the new disc 2 position plus or minus the tooth width, then disc 1 will be set to the new disc 2 position + the tooth width. All values will be normalized to be between o and 359, inclusive. Note: Realistically, this method would not be part of a public interface, since normally the disc positions could not be directly manipulated by the user of the lock. It is made public to simplify development and testing. Parameters: nl - position for disc 1 n2-position for disc 2 n3 - position for disc 3











