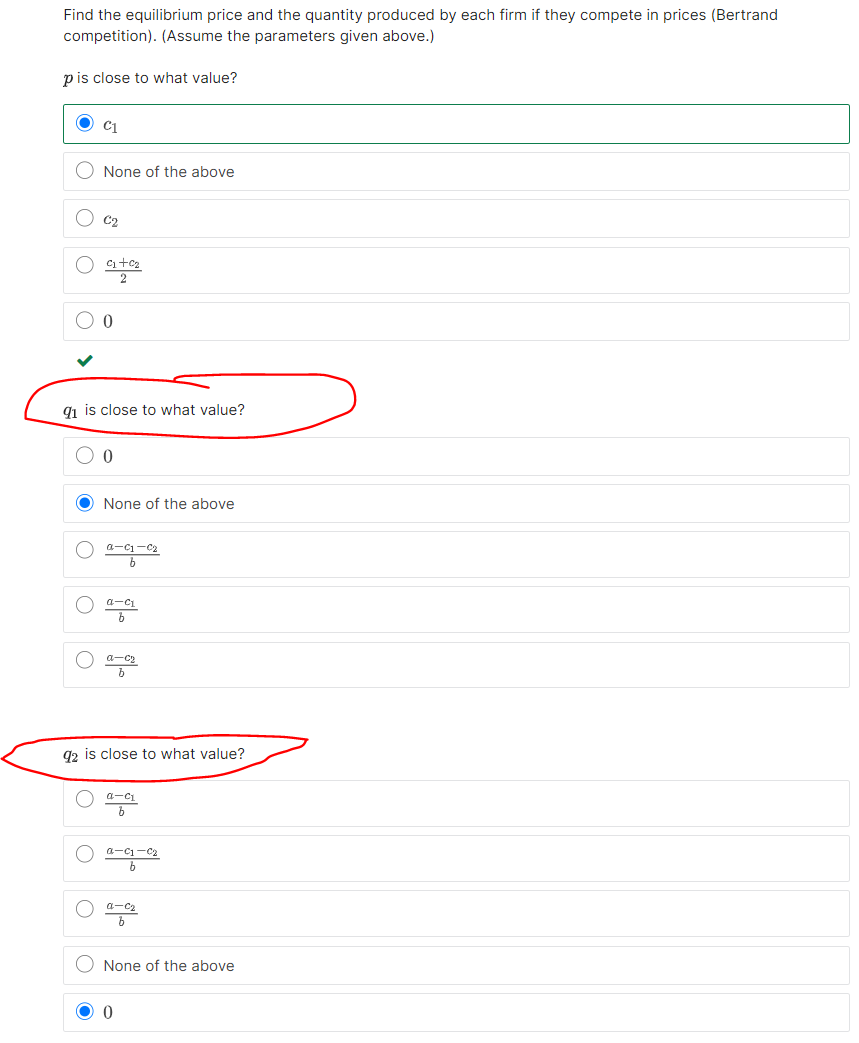
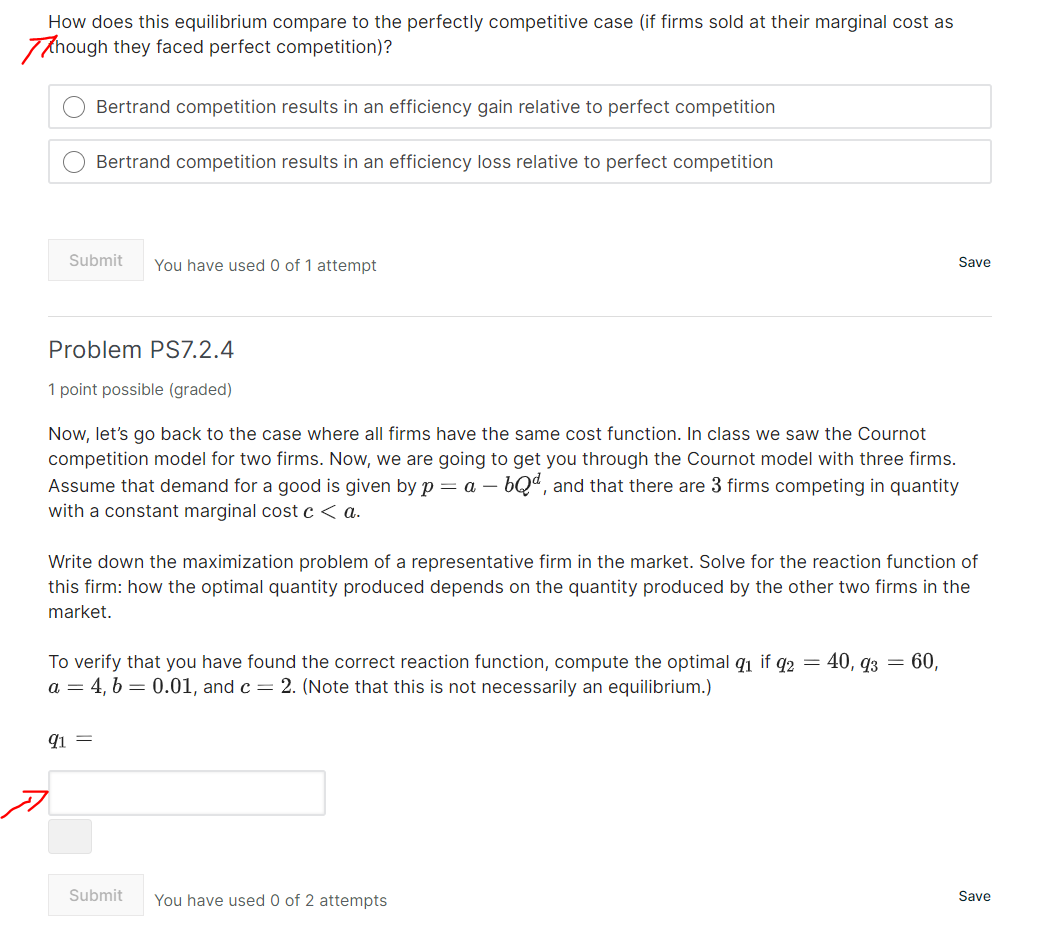
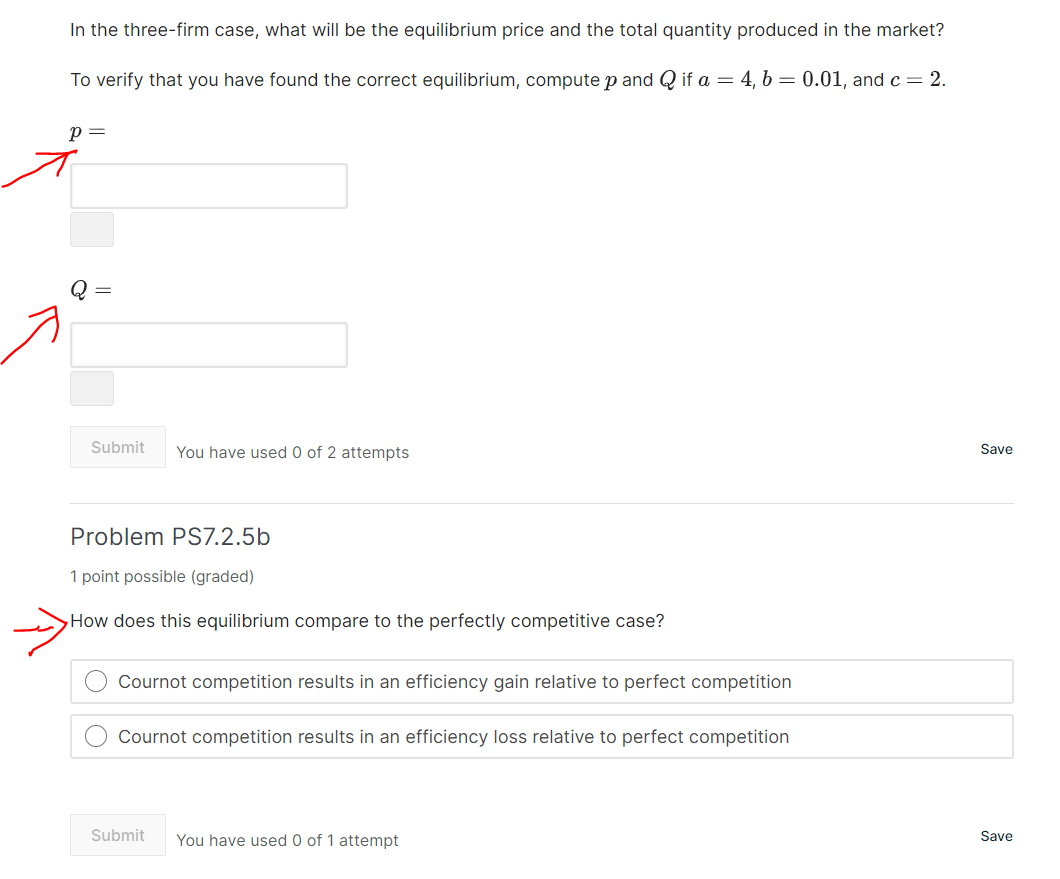
In lecture we saw the Cournot competition model for two firms with the same cost function. Now, we are going to consider asymmetric cost functions. Assume that demand for a good is given byp : a de [Qd is quantity demanded), and that there are 2 firms competing in quantities. Both have no fixed costs and a constant marginal cost. Firm 1 has a marginal cost cl, and firm 2 has a marginal cost c2. We have that a>61>62. Find the reaction functions of firms 1 and 2 in this market: how the optimal quantity produced depends on the quantity produced by the other firm. To verify that you have found the correct reaction functions, compute the optimal (11 if (12 = 100, a = 4, b = 0.01, c1 = 2, and c2 = 1. (Note that this is not necessarily an equilibrium.) 9'1: - 50 Solve for the quantity produced by each firm and the equilibrium price. To verify that you have found the correct equilibrium, compute qi, g3, and 13* if a. = 4, b = 0.01.61 = 2, and 2.3333 v 2.3333 Sme\" You have used 2 of 2 attempts Show answer Find the equilibrium price and the quantity produced by each firm if the}.r compete in prices [Bertrand competition]. [Assume the parameters given above} 3} is close to what value? @Cl 0 None of the above O 02 Q n+0; 2 00 if 9'1 is close to what value? 00 None of the above O acl ::2 b Cg 0 None of the above U How does this equilibrium compare to the perfectly competitive case (if firms sold at their marginal cost as \"bough they faced perfect competition)? 0 Bertrand competition results in an efficiency gain relative to perfect competition 0 Bertrand competition results in an efficiency loss relative to perfect competition Submit You have used 0 of 1 attempt save Problem P8724 1 point possible [graded] Now, let's go back to the case where all firms have the same cost function. In class we saw the Cournot competition model for two firms. Now, we are going to get you through the Cournot model with three firms. Assume that demand for a good is given byp = o. bQ'i, and that there are 3 firms competing in quantity with a constant marginal cost (3 How does this equilibrium compare to the perfectly competitive case? 0 Cournot competition results in an efficiency gain relative to perfect competition 0 Cournot competition results in an efficiency loss relative to perfect competition Smeit You have used 0 of i attempt save lntuitively, what will happen in this market when the number of firms goes to Do? _..> O The market converges to perfect competition 0 None of the above 0 Efficiency losses become arbitrarily large 0 Cournot competition will become the more realistic model C] Price will approach zero Submit You have used 0 of 2 attempts Save