In Matlab.

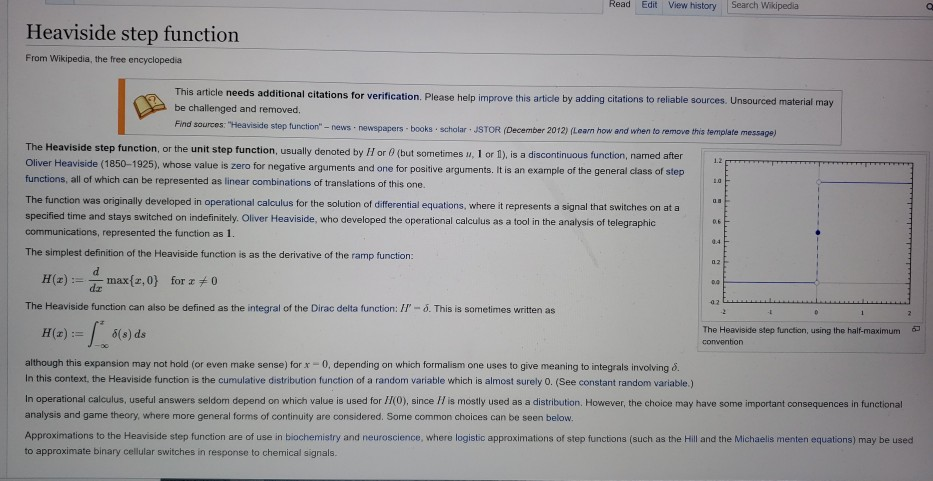
3. (10 points) Computer project: find a least square polynomial approxima- tion of f(1) = H(r) (the heaviside function) on the interval (-1,1], min (f(x) P()da Use the composite Trapezoid rule with 100 quadrature points to approx- imate the integrals. Show the graphs of approximating polynomials for n = 10, 20, 30. Compare them to the graph of f (2). Read Edit View history Search Wikipedia Heaviside step function From Wikipedia, the free encyclopedia This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed. Find sources: "Heavis de step function" -rws.newspapers books scholar JSTOR (December 2012) Learn how and when to remove this template message The Heaviside step function, or the unit step function, usually denoted by H or (but sometimes w 1 or 1) is a discontinuous function, named after Oliver Heaviside (1850-1925), whose value is zero for negative arguments and one for positive arguments. It is an example of the general class of step functions, all of which can be represented as linear combinations of translations of this one. The function was originally developed in operational calculus for the solution of differential equations, where it represents a signal that switches on at a specified time and stays switched on indefinitely, Oliver Heaviside, who developed the operational calculus as a tool in the analysis of telegraphic communications, represented the function as 1. The simplest definition of the Heaviside function is as the derivative of the ramp function: H(x):= max{z,0} for: #0 The Heaviside function can also be defined as the integral of the Dirac delta function: I/' - d. This is sometimes written as H(2):= 6(s) ds The Heaviside step function, using the half-maximum convention although this expansion may not hold (or even make sense) for x-0, depending on which formalism one uses to give meaning to integrals involving 8. In this context, the Heaviside function is the cumulative distribution function of a random variable which is almost surely 0. (See constant random variable.) In operational calculus, useful answers seldom depend on which value is used for 1(0), since I is mostly used as a distribution. However, the choice may have some important consequences in functional analysis and game theory, where more general forms of continuity are considered. Some common choices can be seen below. Approximations to the Heaviside step function are of use in biochemistry and neuroscience, where logistic approximations of step functions (such as the Hill and the Michaelis menten equations may be used to approximate binary cellular switches in response to chemical signals. 3. (10 points) Computer project: find a least square polynomial approxima- tion of f(1) = H(r) (the heaviside function) on the interval (-1,1], min (f(x) P()da Use the composite Trapezoid rule with 100 quadrature points to approx- imate the integrals. Show the graphs of approximating polynomials for n = 10, 20, 30. Compare them to the graph of f (2). Read Edit View history Search Wikipedia Heaviside step function From Wikipedia, the free encyclopedia This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed. Find sources: "Heavis de step function" -rws.newspapers books scholar JSTOR (December 2012) Learn how and when to remove this template message The Heaviside step function, or the unit step function, usually denoted by H or (but sometimes w 1 or 1) is a discontinuous function, named after Oliver Heaviside (1850-1925), whose value is zero for negative arguments and one for positive arguments. It is an example of the general class of step functions, all of which can be represented as linear combinations of translations of this one. The function was originally developed in operational calculus for the solution of differential equations, where it represents a signal that switches on at a specified time and stays switched on indefinitely, Oliver Heaviside, who developed the operational calculus as a tool in the analysis of telegraphic communications, represented the function as 1. The simplest definition of the Heaviside function is as the derivative of the ramp function: H(x):= max{z,0} for: #0 The Heaviside function can also be defined as the integral of the Dirac delta function: I/' - d. This is sometimes written as H(2):= 6(s) ds The Heaviside step function, using the half-maximum convention although this expansion may not hold (or even make sense) for x-0, depending on which formalism one uses to give meaning to integrals involving 8. In this context, the Heaviside function is the cumulative distribution function of a random variable which is almost surely 0. (See constant random variable.) In operational calculus, useful answers seldom depend on which value is used for 1(0), since I is mostly used as a distribution. However, the choice may have some important consequences in functional analysis and game theory, where more general forms of continuity are considered. Some common choices can be seen below. Approximations to the Heaviside step function are of use in biochemistry and neuroscience, where logistic approximations of step functions (such as the Hill and the Michaelis menten equations may be used to approximate binary cellular switches in response to chemical signals