In part B answer it states the initial bundle of A is 50 shoes and the final bundle is 33.33 shoes. What is the process to find these numbers?
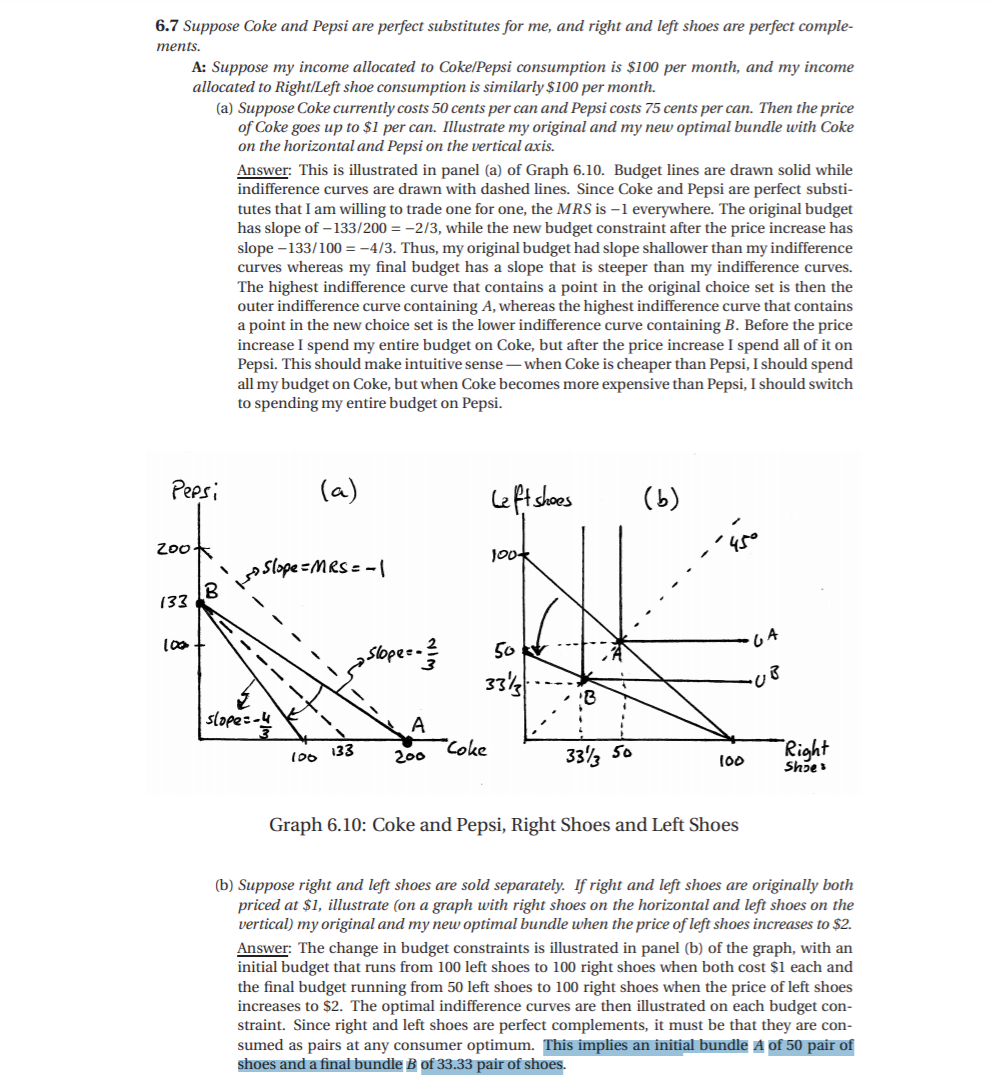
6.7 Suppose Coke and Pepsi are perfect substitutes for me, and right and left shoes are perfect comple- ments. A: Suppose my income allocated to Coke/Pepsi consumption is $100 per month, and my income allocated to Right/Left shoe consumption is similarly $100 per month. (a) Suppose Coke currently costs 50 cents per can and Pepsi costs 75 cents per can. Then the price of Coke goes up to $1 per can. Illustrate my original and my new optimal bundle with Coke on the horizontal and Pepsi on the vertical axis. Answer: This is illustrated in panel (a) of Graph 6.10. Budget lines are drawn solid while indifference curves are drawn with dashed lines. Since Coke and Pepsi are perfect substi tutes that I am willing to trade one for one, the MRS is -1 everywhere. The original budget has slope of -133/200 = -2/3, while the new budget constraint after the price increase has slope -133/100 = -4/3. Thus, my original budget had slope shallower than my indifference curves whereas my final budget has a slope that is steeper than my indifference curves. The highest indifference curve that contains a point in the original choice set is then the outer indifference curve containing A, whereas the highest indifference curve that contains a point in the new choice set is the lower indifference curve containing B. Before the price increase I spend my entire budget on Coke, but after the price increase I spend all of it on Pepsi. This should make intuitive sense - when Coke is cheaper than Pepsi, I should spend all my budget on Coke, but when Coke becomes more expensive than Pepsi, I should switch to spending my entire budget on Pepsi. Pepsi ( a) Left shoes ( b ) Slope = MRS = - 1 18 100 - 64 Slopes - 2 50 slope =-4 A 100 133 200 Coke 33/3 50 Right 100 Shoe s Graph 6.10: Coke and Pepsi, Right Shoes and Left Shoes (b) Suppose right and left shoes are sold separately. If right and left shoes are originally both priced at $1, illustrate (on a graph with right shoes on the horizontal and left shoes on the vertical) my original and my new optimal bundle when the price of left shoes increases to $2. Answer: The change in budget constraints is illustrated in panel (b) of the graph, with an initial budget that runs from 100 left shoes to 100 right shoes when both cost $1 each and the final budget running from 50 left shoes to 100 right shoes when the price of left shoes increases to $2. The optimal indifference curves are then illustrated on each budget con- straint. Since right and left shoes are perfect complements, it must be that they are con- sumed as pairs at any consumer optimum. This implies an initial bundle A of 50 pair of shoes and a final bundle B of 33.33 pair of shoes