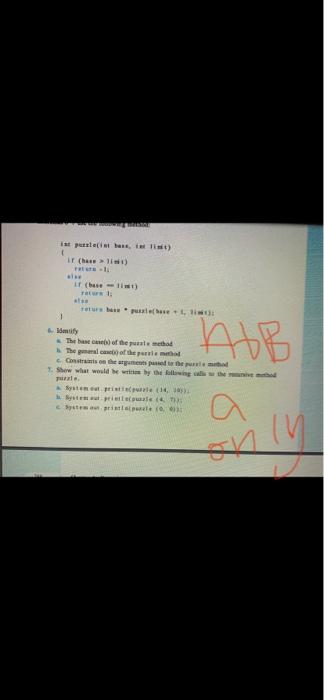
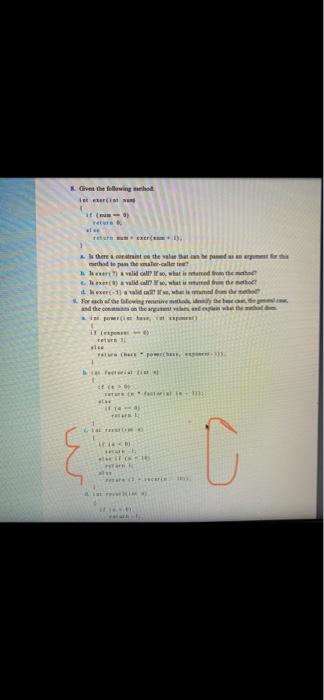
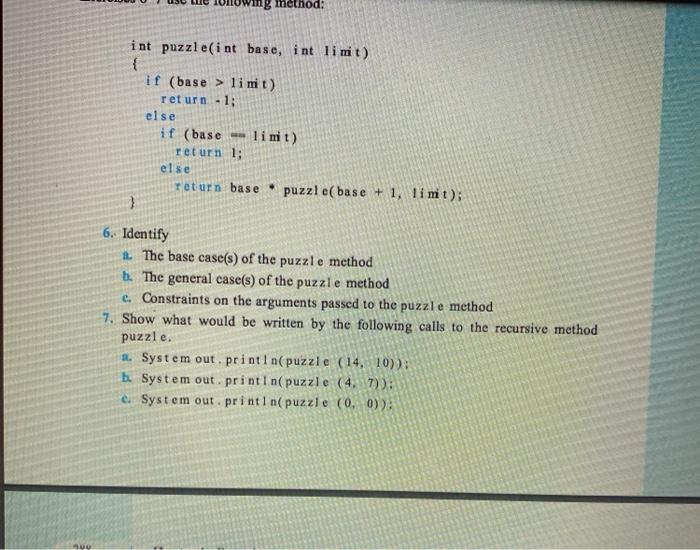
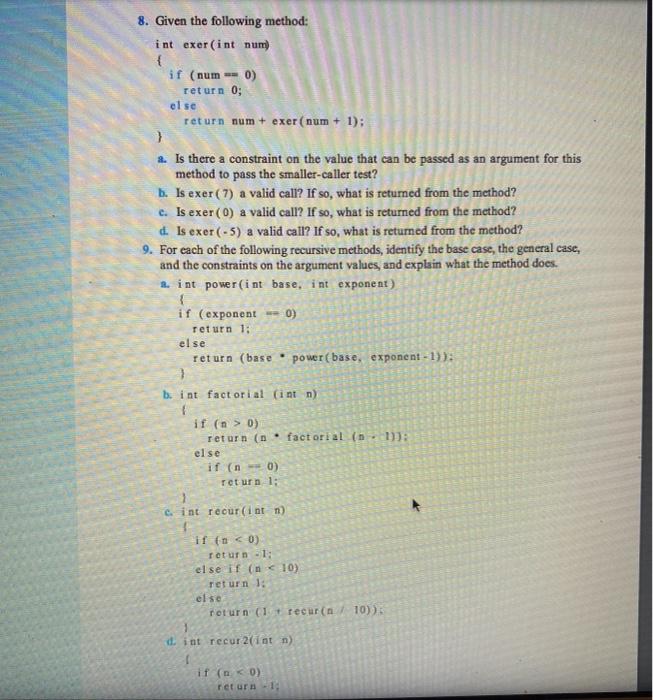
in putelei hanelist) ir (hare) if (huset) as 1 AB tity The base of the pule method The goal of them - Onia so the argumentum 1. Show what would be by the theme Tuale Seile (14) 40 risparate ly Give the following IM res et (1) the content that the call 1.), white ) vida, who L-1), where Forschuhe and the other the net IT (R) 1 see (h. Festi Roma O - HIM mg method: int puzzle(int base, int limit) { if (base > limit) return -1; else if (base - limit) return 1; else return base puzzle(base + 1, limit); 3 6. Identify 1. The base case(s) of the puzzle method b. The general case(s) of the puzzle method e Constraints on the arguments passed to the puzzle method 7. Show what would be written by the following calls to the recursive method puzzle. 1. System out.println(puzzle (14, 10)): b System out.println(puzzle (4. 7)): e. System out.println(puzzle (0, 0)) 8. Given the following method: int exer(int num) { if (num 0) return 0; el se return num+ exer(num + 1): } 2. Is there a constraint on the value that can be passed as an argument for this method to pass the smaller-caller test? b. Is exer(7) a valid call? If so, what is returned from the method? e. Is exer (0) a valid call? If so, what is returned from the method? d. Is exer(-5) a valid call? If so, what is returned from the method? 9. For each of the following recursive methods, identify the base case, the general case, and the constraints on the argument values, and explain what the method does. 2. int power (int base, int exponent) if (exponent -- 0) return 1; else return (base power (base, exponent-1)): b. int factorial (int n) if (n > 0) return factorial (n. 1): else if (n-0) return 1: cint recur (int n) if in limit) return -1; else if (base - limit) return 1; else return base puzzle(base + 1, limit); 3 6. Identify 1. The base case(s) of the puzzle method b. The general case(s) of the puzzle method e Constraints on the arguments passed to the puzzle method 7. Show what would be written by the following calls to the recursive method puzzle. 1. System out.println(puzzle (14, 10)): b System out.println(puzzle (4. 7)): e. System out.println(puzzle (0, 0)) 8. Given the following method: int exer(int num) { if (num 0) return 0; el se return num+ exer(num + 1): } 2. Is there a constraint on the value that can be passed as an argument for this method to pass the smaller-caller test? b. Is exer(7) a valid call? If so, what is returned from the method? e. Is exer (0) a valid call? If so, what is returned from the method? d. Is exer(-5) a valid call? If so, what is returned from the method? 9. For each of the following recursive methods, identify the base case, the general case, and the constraints on the argument values, and explain what the method does. 2. int power (int base, int exponent) if (exponent -- 0) return 1; else return (base power (base, exponent-1)): b. int factorial (int n) if (n > 0) return factorial (n. 1): else if (n-0) return 1: cint recur (int n) if in