In Python
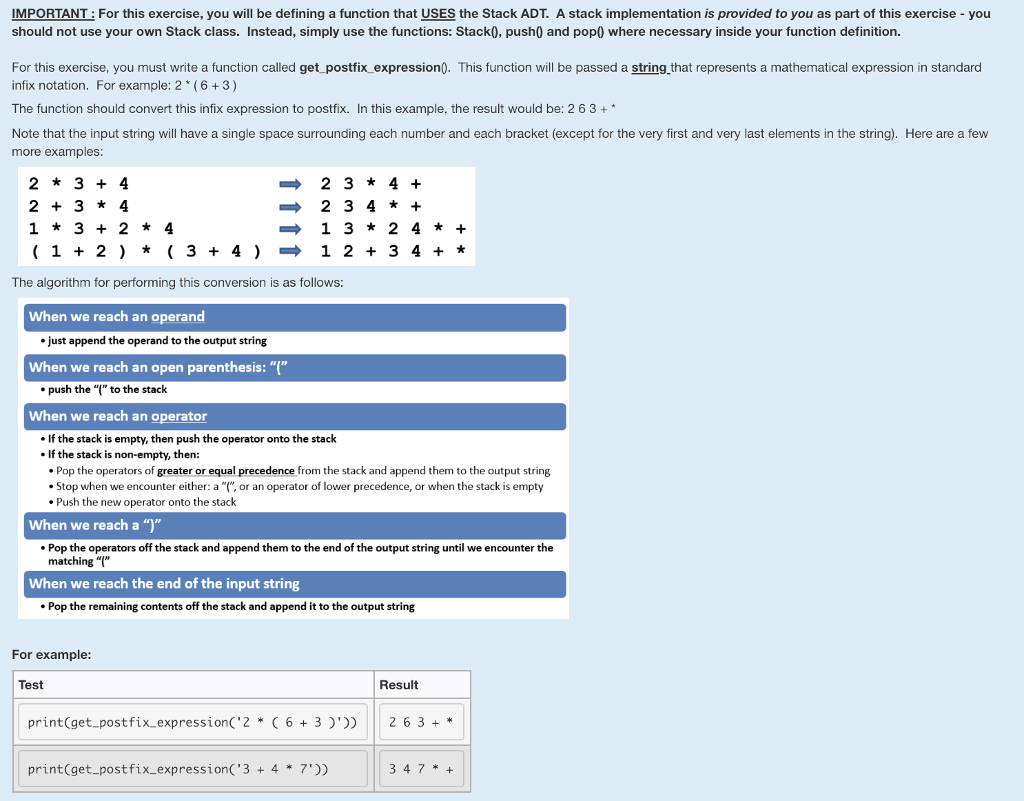
IMPORTANT: For this exercise, you will be defining a function that USES the Stack ADT. A stack implementation is provided to you as part of this exercise you should not use your own Stack class. Instead, simply use the functions: Stack0, push0 and pop where necessary inside your function definition. For this exercise, you must rite a function called get_ postfix expression. This function will be passed a string that represents a mathematical expression in standard infix notation. For example: 2 (63) The function should convert this infix expression to postfix. In this example, the result would be: 2 6 3 + Note that the input string will have a single space surrounding each number and each bracket (except for the very first and very last elements in the string). Here are a few more examples: 2 t 3 2 + 3 1 t3 4 4 2 * 4 2 3 4 + The algorithm for performing this conversion is as follows When we reach an operand .just append the operand to the output string When we reach an open parenthesis: "(" .push the "" to the stack When we reach an operator If the stack is empty, then push the operator onto the stack If the stack is non-empty, then: Pop the operators of greater or equal precedence from the stack and append them to the output string Stop when we encounter either: a or an operator of lower precedence, or when the stack is empty Push the new operator onto the stack When we reach a "" Pop the operators off the stack and append them to the end of the output string until we encounter the matching " When we reach the end of the input string . Pop the remaining contents off the stack and append it to the output string For example Test Result print(get_postfix_expression('26 3)') 26 3 * print(get_postfix_expression('3 47)) 3 47*+ IMPORTANT: For this exercise, you will be defining a function that USES the Stack ADT. A stack implementation is provided to you as part of this exercise you should not use your own Stack class. Instead, simply use the functions: Stack0, push0 and pop where necessary inside your function definition. For this exercise, you must rite a function called get_ postfix expression. This function will be passed a string that represents a mathematical expression in standard infix notation. For example: 2 (63) The function should convert this infix expression to postfix. In this example, the result would be: 2 6 3 + Note that the input string will have a single space surrounding each number and each bracket (except for the very first and very last elements in the string). Here are a few more examples: 2 t 3 2 + 3 1 t3 4 4 2 * 4 2 3 4 + The algorithm for performing this conversion is as follows When we reach an operand .just append the operand to the output string When we reach an open parenthesis: "(" .push the "" to the stack When we reach an operator If the stack is empty, then push the operator onto the stack If the stack is non-empty, then: Pop the operators of greater or equal precedence from the stack and append them to the output string Stop when we encounter either: a or an operator of lower precedence, or when the stack is empty Push the new operator onto the stack When we reach a "" Pop the operators off the stack and append them to the end of the output string until we encounter the matching " When we reach the end of the input string . Pop the remaining contents off the stack and append it to the output string For example Test Result print(get_postfix_expression('26 3)') 26 3 * print(get_postfix_expression('3 47)) 3 47*+







