in pytnon

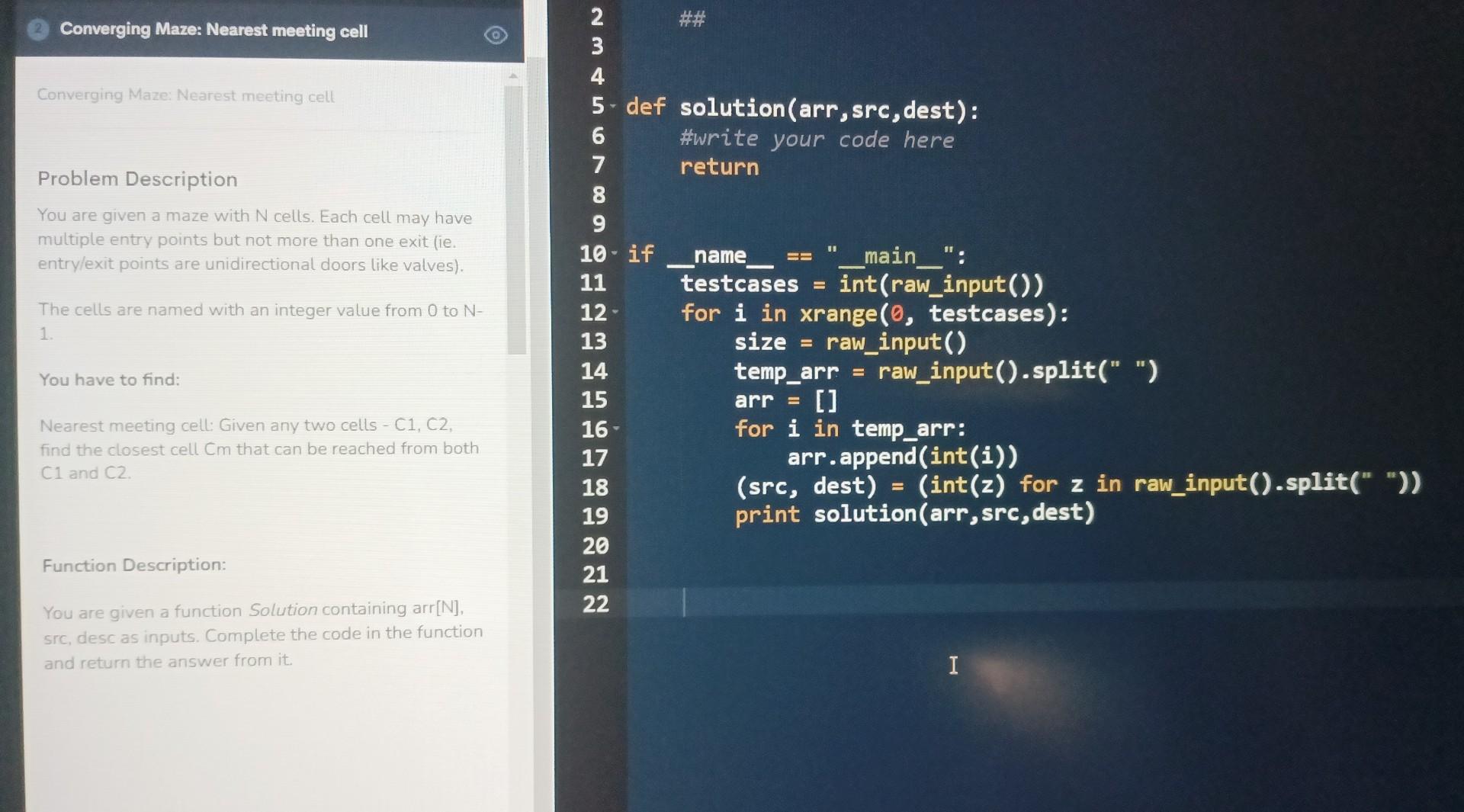
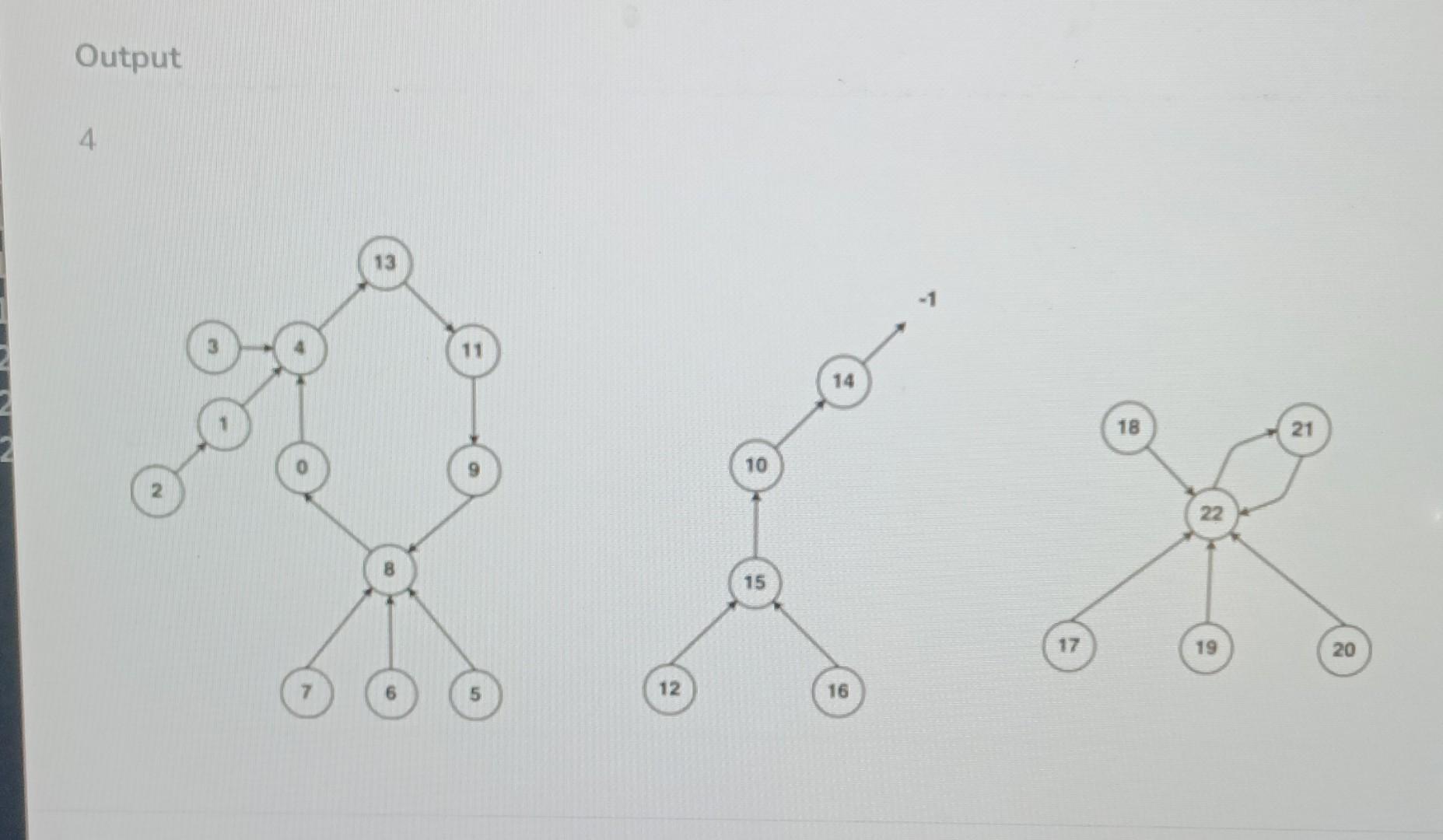
(2) Converging Maze: Nearest meeting cell Converging Maze: Nearest meeting cell Problem Description You are given a maze with N cells. Each cell may have multiple entry points but not more than one exit (ie. entry/exit points are unidirectional doors like valves). The cells are named with an integer value from 0 to N - 1. You have to find: Nearest meeting cell: Given any two cells - C1, C2, 16. 15 for i in temp_arr: find the closest cell Cm that can be reached from both arr. append (int (i)) (src, dest) =( int (z) for z in raw_input().split(" ")) print solution(arr, src, dest) Function Description: You are given a function Solution containing arr [N], src, desc as inputs. Complete the code in the function and return the answer from it. 1. An integer T, denoting the number of testcases, followed by 3T lines, as each testcase will contain 3 lines. 2. The first line of each testcase has the number of cells N 3. The second line of each testcase has a list of N values of the edge[] array. edge[i] contains the cell number that can be reached from cell ' i ' in one step. edge[i] is 1 if the 'i'th cell doesn't have an exit. 4. Third line for each testcase contains two cell numbers whose nearest meeting cell needs to be found. (return 1 if there is no meeting cell from the two given cells) OUTPUT FORMAT For each testcase given, output a single line that denotes the nearest meeting cell (NMC) Sample Input \& Output Input 1 23 44141388808149151111015222222222221 92 Output 4