In the articleCoffee, Caffeine, and Risk of Depression Among Womenin the September 2011 edition of the Archives of Internal Medicine, researchers investigated the relationship between caffeine consumption and depression among women.
The participants in this study were older, with substantially lower rates of depression when compared to female teens. Researchers compared two groups of women (among others) in this study: those who do not drink coffee and those who routinely drink 4 or more cups of coffee each day.
For the following question, acoffee drinkeris a woman who drinks four or more cups each day.
The depression rate for women who do not drink coffee is 6%. For the moment, we assume that this is the rate for coffee drinkers as well. We plan to survey 920 women who drink coffee and 1100 women who do not. We will determine the proportion of women who are depressed in each sample.
Will the sampling distribution of differences between sample proportions be approximately normal?
- Yes, a normal model is a good fit for this sampling distribution.
- No, a normal model is not a good fit for this sampling distribution.
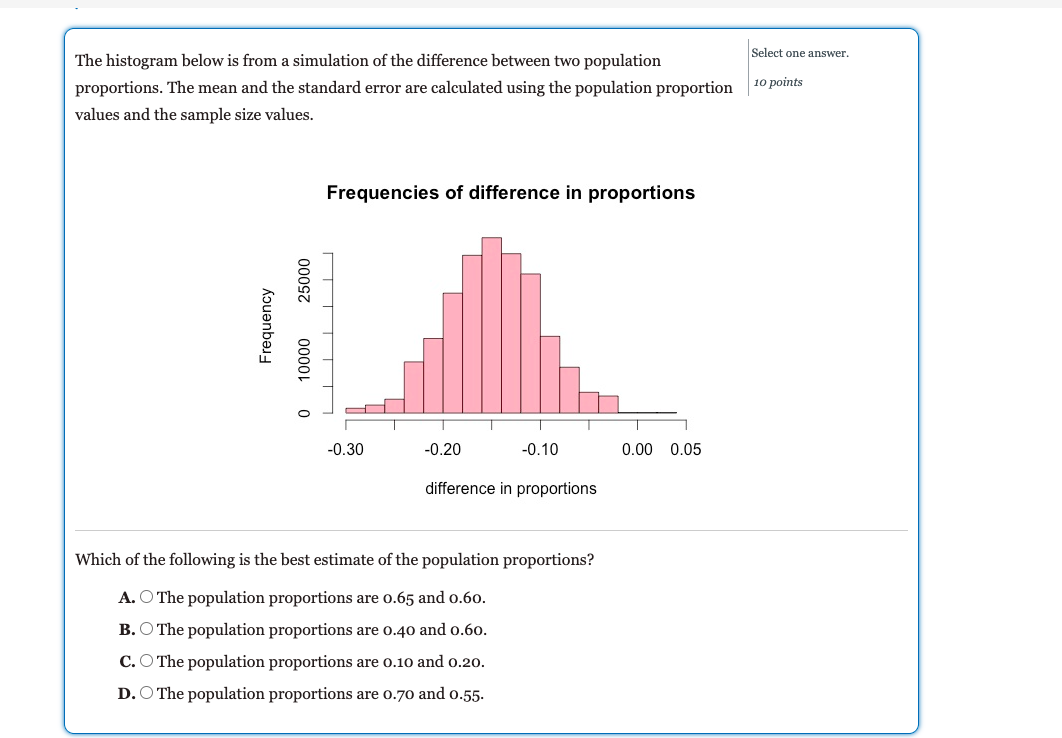
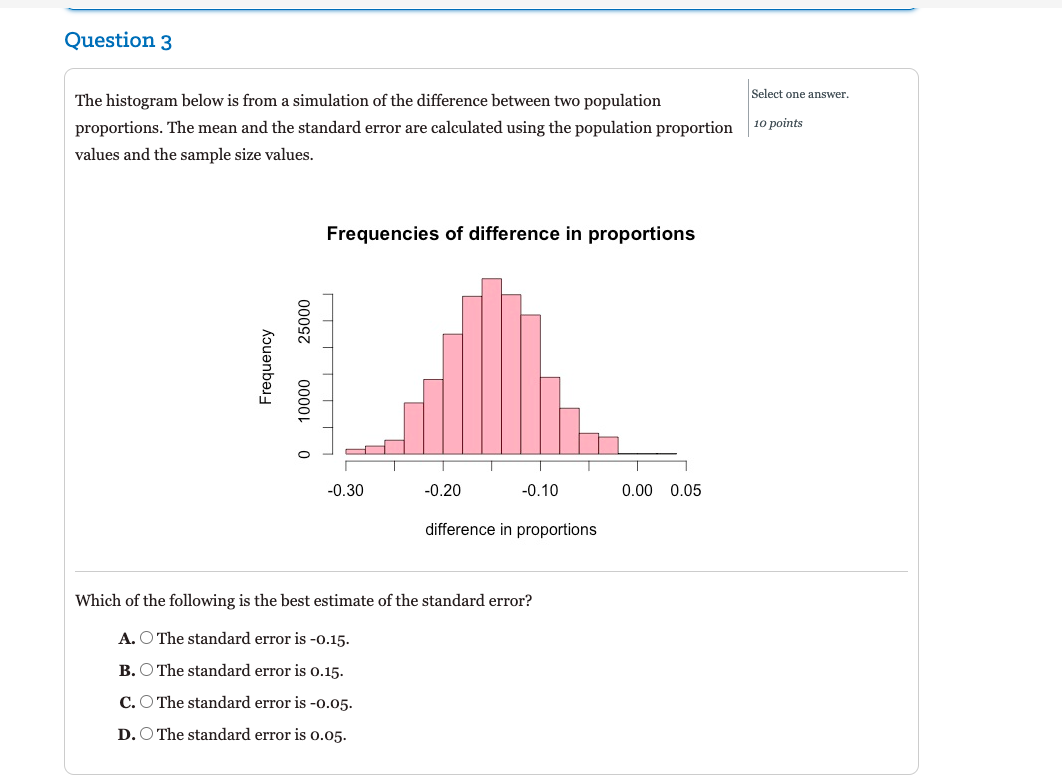
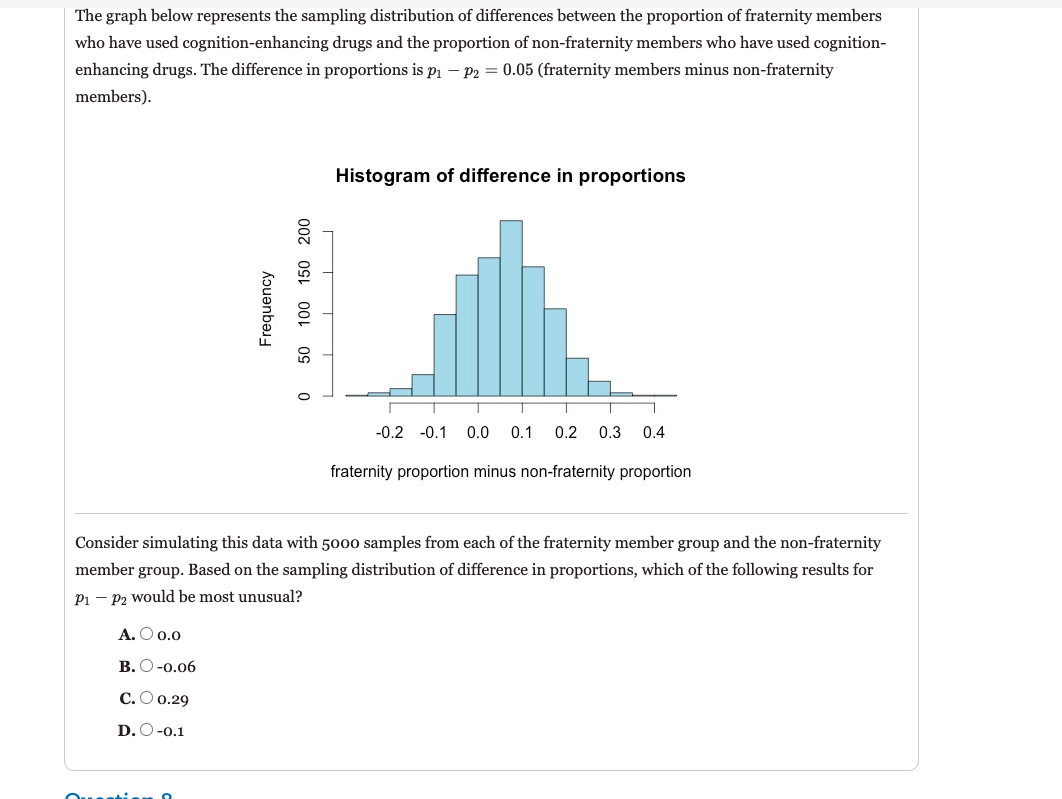
The histogram below is from a simulation of the difference between two population proportions. The mean and the standard error are calculated using the population proportion values and the sample size values. Frequencies of difference in proportions llIlIIll 41.20 -D.10 {1.00 0.05 difference in proportions 'Whieh of the following is the best estimate of the population proportions? A. O The population proportions are 0.65 and 0.60. B. O The population proportions are 0.40 and 0.60. C. O The population proportions are 0.10 and 0.20. D. O The population proportions are 0.70 and 0.55. Question 3 The histogram below is from a simulation of the difference between two population Select one answer. proportions. The mean and the standard error are calculated using the population proportion 10 points values and the sample size values. Frequencies of difference in proportions 25000 Frequency 10000 O -0.30 -0.20 -0.10 0.00 0.05 difference in proportions Which of the following is the best estimate of the standard error? A. O The standard error is -0.15. B. O The standard error is 0.15. C. O The standard error is -0.05. D. O The standard error is 0.05.The graph below represents the sampling distribution of differences between the proportion of fraternity members who have used cognition-enhancing drugs and the proportion of non-fraternity members who have used cognition- enhancing drugs. The difference in proportions is 1.31 p2 = 0.05 (fraternity members minus non-fratemity members). Histogram of difference in proportions D Q_ N 522- 5 O LL 8- a- llIllll -D.2 -0.1 0.0 0.1 0.2 0.3 {1.4 fraternity proportion minus non-fratemity proportion Consider simulating this data with 5000 samples from each of the fraternity member group and the non-fraternity member group. Based on the sampling distribution of difference in proportions, which of the following results for p1 112 would be most unusual? A. O 0.0 B. O -o.06 C. O 0.29 D. O -o.1 n--__;.:___ n Histogram of difference in proportions O ._ N 0 {3'2 5 Q LL 8- ._ lllllll -0.2 -0.1 0.0 0.1 {1.2 0.3 0.4 fraternity proportion minus non-fratemity proportion The difference in proportions is p1 - p2 = 0.05 [fraternity members minus non-fraternity members], and the standard error is 0.08. The z~score for this difference in sample proportions is 0.885. 'Which of the following is the most appropriate conclusion? A. Q There is a statistically signicant difference between the proportion of fraternity members who have used cognition-enhancing drugs and the proportion of no n-fraternity members who have used cognition- enhancing drugs. B. Q There is not a statistically signicant difference between the proportion of fraternity members who have used cognition-enhancing drugs and the proportion of non-fraternity members who have used cognition- enhancing drugs. C. 0 We do not have enough information to make a conclusion about the difference between the proportion of fraternity members who have used cognition-enhancing drugs and the proportion of non-fraternity members who have used cognition-enhancing drugs. In the article "Coffee, Caffeine, and Risk of Depression Among Women" in the September 2011 Select one answer. edition of the Archives of Internal Medicine, researchers investigated the relationship between 10 points caffeine consumption and depression among women. The participants in this study were older, with substantially lower rates of depression when compared to female teens. Researchers compared two groups of women (among others) in this study: those who do not drink coffee and those who routinely drink 4 or more cups of coffee each day. For the following question, a coffee drinker is a woman who drinks four or more cups each day. One of the graphs below represents the sampling distribution of differences between the sample proportions for depressed coffee and non-coffee drinking women. Under the assumption that both women who drink coffee and do not drink coffee have a 6% depression rate, which distribution of differences in sample proportions is centered correctly? A -0.03+ 0.04+ -0.04- 0.0 0.02 -0.02- 0.01 -0.01 0.03 BB. O Graph B A. O Graph A C. O Graph C -0.1 + 0.02+ B C -0.09- 0.03 - -0.08 - 0.04 0.05 So the statistic is the sample proportion for coffee drinkers minus the sample proportion for non-coffee drinkers. -0.07 -0.06 0.06- 0.05 0.07 -0.04- 0.08 -0.03 0.09 -0.02- 0.1 +