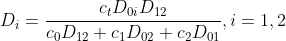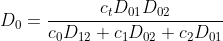In the book Electrochemical Engineering I by Ivo Rousar ISBN 0-444-99562-5 an effective binary diffusion coefficient is established for a three-species system. Enclosed are the two pages 33 and 34 with corresponding justifications. I am trying to understand mathematically how he gets from Eq. (2.1.5) to Eq. (2.2.1) with the specific diffusion coefficients?
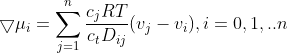 (2.1.5)
(2.1.5)
More specifically, how do I solve the sum of (2.1.5) for three species, where one species i=0 is the solvent and one equation can be omitted ?where 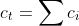 and
and 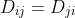 are transport parameters of the dimension of diffusion coefficients, characterizing interactions between the species i and j. They are defined only for ij and are independent of the coordinate system to which the velocities vi are referred, since Eq. (2.1.5) involves only the differences of the velocities. However after this he shall consider a system containing three species: the solvent (i = 0), cations (i= 1), and anions (i = 2). Since the system of equations (2.1.5) is linearly interdependent, he drop one equation, say for i = 0. But I do not understand how he came mathematically to the following equations:
are transport parameters of the dimension of diffusion coefficients, characterizing interactions between the species i and j. They are defined only for ij and are independent of the coordinate system to which the velocities vi are referred, since Eq. (2.1.5) involves only the differences of the velocities. However after this he shall consider a system containing three species: the solvent (i = 0), cations (i= 1), and anions (i = 2). Since the system of equations (2.1.5) is linearly interdependent, he drop one equation, say for i = 0. But I do not understand how he came mathematically to the following equations:
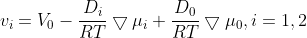 (2.2.1)
(2.2.1)
where the new diffusion coefficients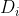 are defined as:
are defined as:
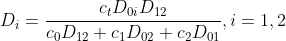
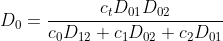


2. TRANSPORT EQUATIONS FOR CONCENTRATED ELECTROLYTES 2.1 Basic equations In this section, we shall deal with a more accurate phenomenological theory of the transport of ions in electrolyte solutions (disregarding the molecular properties of the components). To this end, we must abandon the basic assumption of the theory of transport in dilute electrolytes, namely that of the independent diffusion of all solution components. Indeed, for example, in a solution containing two different electrolytes two different concentration gradients can be formed between which there is no simple linkage as in the case of a single binary electrolyte, and the diffusion flux of each component can be influenced by both gradients. Generally, interactions of all components (solvent and ions) with one another can be expected. These interactions are taken into account by the theory of transport based on the thermodynamics of irreversible processes 13. We shall consider an isothermal system consisting of the solvent (concentration c0 and velocity v0 ) and n dissolved species (ions or perhaps nonelectrolytes; concentrations c1 through cn and velocities v1 through vn ). The individual fluxes are expressed according to irreversible thermodynamics as linear functions of "thermodynamic" forces Xj Ji=civi=j=1nlijXj. The fluxes are referred to the solvent, hence v0=0;lij are phenomenological transport coefficients, which fulfil the Onsager reciprocal relations lij=ljl,i,j=1,2,,n. The thermodynamic forces Xj are expressed in terms of chemical or electrochemical potentials as xj=j and they are linearly dependent according to the Gibbs-Duhem relation i=0nciXi=0. All transport properties of a given solution, namely electric conductivity, transference numbers, and diffusion coefficients can be calculated from the coefficients Iij and vice versa, from these transport properties the coefficients lij can be determined. However, the calculations become increasingly more complicated with the increasing number of species n; and only the cases of binary and ternary electrolytes have been dealt with in the literature 1,2. For practical reasons, other transport parameters. Dij. have been introduced, by analogy to diffusion coeflicients 35. To show their significance, we solve the system of equations (2.1.1) with respect to Xj : after rearrangement we obtain j=j=1nctDijcjRT(vjvi),i=0,1,,n, where c1=ci and Dij=Dji are transport parameters of the dimension of diffusion coefficients, characterizing interactions between the species i and j. They are defined only for i=j and are independent of the coordinate system to which the velocities vi are referred, since Eq. (2.1.5) involves only the differences of the velocities. 2.2 Binary electrolyte We shall consider a system containing three species: the solvent (i=0), cations (i=1), and anions (i=2). Since the system of equations (2.1.5) is linearly interdependent, we must drop one equation, say for i=0. Then we have only two equations left, from which the velocities v1 and v2 or fluxes J1 and J2 can be calculated. Since the electrochemical potentials fulfil the relation (2.1.4), the solution can be written in the form vi=v0RTDii+RTD00,i=1,2, where the new diffusion coefficients Di are defined as Di=c0D12+c1D02+c2D01ctD01D12,i=1,2,D0=c0D12+c1D02+c2D01ctD01D02. Further we obtain an expression for the electric current density in the solution, j=c1F1(v1v2) j=F(z1t11+z2t22)
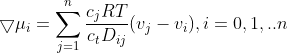 (2.1.5)
(2.1.5)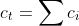 and
and 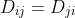 are transport parameters of the dimension of diffusion coefficients, characterizing interactions between the species i and j. They are defined only for ij and are independent of the coordinate system to which the velocities vi are referred, since Eq. (2.1.5) involves only the differences of the velocities. However after this he shall consider a system containing three species: the solvent (i = 0), cations (i= 1), and anions (i = 2). Since the system of equations (2.1.5) is linearly interdependent, he drop one equation, say for i = 0. But I do not understand how he came mathematically to the following equations:
are transport parameters of the dimension of diffusion coefficients, characterizing interactions between the species i and j. They are defined only for ij and are independent of the coordinate system to which the velocities vi are referred, since Eq. (2.1.5) involves only the differences of the velocities. However after this he shall consider a system containing three species: the solvent (i = 0), cations (i= 1), and anions (i = 2). Since the system of equations (2.1.5) is linearly interdependent, he drop one equation, say for i = 0. But I do not understand how he came mathematically to the following equations: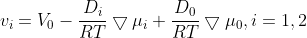 (2.2.1)
(2.2.1)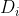 are defined as:
are defined as: