Question
In the case of normally distributed classes, discriminant functions are linear (straight lines, planes, and hyperplanes for two-, three-, and n-dimensional feature vectors, respectively) when
In the case of normally distributed classes, discriminant functions are linear (straight lines, planes, and hyperplanes for two-, three-, and n-dimensional feature vectors, respectively) when the covariances matrices of corresponding classes are equal. Confirm this by deriving discriminant functions for a binary classification problem.Given:Prove that linear discriminant functionsAnd decision boundary g(x) = g1(x) - g2(x) = 0 is given by(Hint: Use equations 3.61-3.62 in the textbook)Part 2Perform two iterations of the gradient algorithm to find the minima ofE(w)=2w21+2w1w2+5w22The starting point isw=[2-2]T
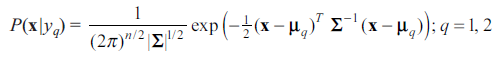
Step by Step Solution
There are 3 Steps involved in it
Step: 1

Get Instant Access to Expert-Tailored Solutions
See step-by-step solutions with expert insights and AI powered tools for academic success
Step: 2

Step: 3

Ace Your Homework with AI
Get the answers you need in no time with our AI-driven, step-by-step assistance
Get Started


