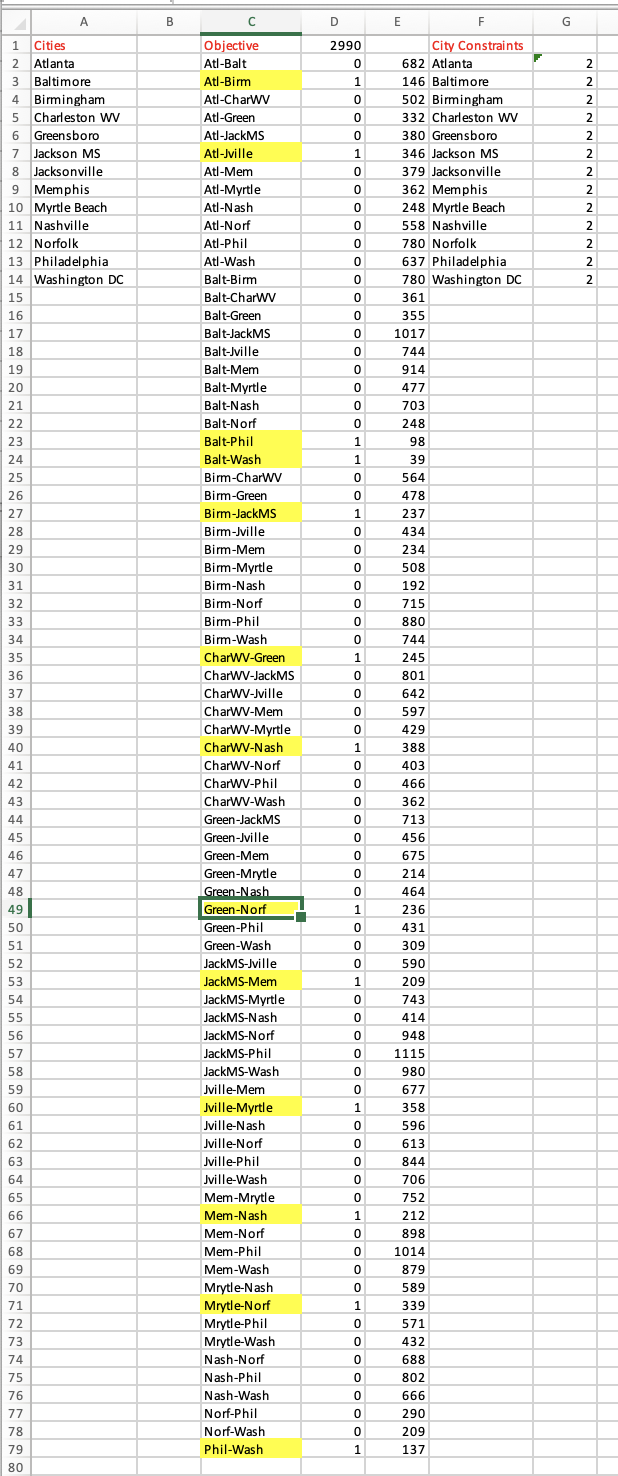
In the first project, we used Excel Solver to minimize cell D$1,$ subject to two constraints: $1)$ G$2$: G$14=2$; and $2)$ D$2$:D$79$ integer. This generated a lower bound on the optimal objective function value of our TSP$,$ but it also introduced subtours: in the case of the first LP$,$ all of the subtours were easily identified since they corresponded to edges with a value of two. The last task on the first project was to require these variables to be thereby eliminating these relatively easy subtours. We solved the resulting LP relaxation, which we called LP$2.$ That$$s where we stopped, but there are more complex subtours still lurking. This project picks up from the solution of LP$2$ in the first project on the Traveling Salesman problem.

$1.$ The solution of LP$2$ should have subtours with multiple arcs. $($If instead you get a solution with more arcs with values greater than $1,$ then add constraints to eliminate these.$)$ The fun $($and somewhat time$-$consuming$)$ part of the project is using the arcs whose values are equal to $1$ to identify the subtours in your solution $($e$.$g$.$ if the first arc $=1,$ then a tour goes directly from Atlanta to Baltimore$).$ Identifying the positive decision variables and connecting the corresponding cities will reveal the subtours that make up the solution to LP$2.$ Find the smallest of these subtours and add a constraint to eliminate it$.$

For example: if cells D$2,$ D$3$ and D$14$ all equal $1,$ this would give a subtour from Atlanta to Baltimore $($D$2)$ to Birmingham $($D$14)$ and back to Atlanta $($D$3).$ You would eliminate this by putting the formula $=$D$2+$D$3+$D$14$ into a cell on your spreadsheet, say G$15,$ and then adding the constraint G Specify the smallest subtour that you found by listing the $3$ cities included in this tour $($similar to the one in the example above: Atlanta to Baltimore to Birmingham to Atlanta, except that the $3-$city subtour that you find makes geographic sense!$).$

Subtour:

$2.$ Create a constraint to eliminate the subtour identified in the previous question and re$-$solve the LP relaxation. Give the optimal objective function of the new LP $($LP$3).$

Optimal objective function value of LP$3$:

$3.$ Repeat the process you just stepped through to identify the smallest subtour from LP$3($it should be similar to the one you just eliminated, but with $4$ cities included instead of $3).$ Add a constraint to eliminate this subtour $($since it has $4$ cities, your constraint should require that the sum of the $4$ arcs in the subtour must be List the arcs in this subtour. After adding the new constraint, solve the resulting LP $($LP$4)$ and record its objective function value.

Arcs in subtour of LP$3$:

Optimal objective function value of LP$4$:

$4.$ Repeat question $3$ two more times. You should find two subtours that are very similar to the one you identified in the previous question. In fact, they should connect the same $4$ cities. Identify the similar subtour in LP$4($by listing its arcs$),$ add the constraint to eliminate it$,$ and record the objective function value of LP$5.$ Do the same thing to identify a subtour in LP$5,$ eliminate it$,$ and give the objective function value of the resulting LP$6.$

Arcs in subtour of LP$4$:

Optimal objective function value of LP$5$:

Arcs in subtour of LP$5$:

Optimal objective function value of LP$6$:

$5.$ Considering the similarities of the previous three subtours that you had to eliminate one at a time, develop a better constraint $($and a better approach$)$ that could eliminate all of the subtours connecting the same $4$ cities all at once?

$6.$ The point of the previous question is that a single constraint could eliminate all subtours connecting the same $4$ cities. Sadly, the total number of possible subtour constraints is combinatorial. How many sets of $4-$city groupings would there be out of $13$ total cities? This number might not seem so huge. But it ramps up quickly. How many sets of $10-$city groupings would there be for a TSP with $100$ total cities?

$7.$ See if you can find the optimal solution to the $13-$city TSP by continuing to eliminate subtours. After solving LP$6,$ all that should be needed is to identify arcs whose LP$6$ solution value equals $2$ and add the constraints to ensure they are See what you can come up with as your best tour, either by continuing to add subtour constraints or by building one yourself using what you have learned from the LP solutions. Provide the tour $($e$.$g Atlanta to Birmingham to $...),$ along with its associated costs.$\backslash$table$[[,$A$,$B$,$c$,D,E,F,$G$],[1,$Cities,,Objective,$2990,,$City Constraints,$],[2,$Atlanta,,Atl$-$Balt,$0,682,$Atlanta,$F$