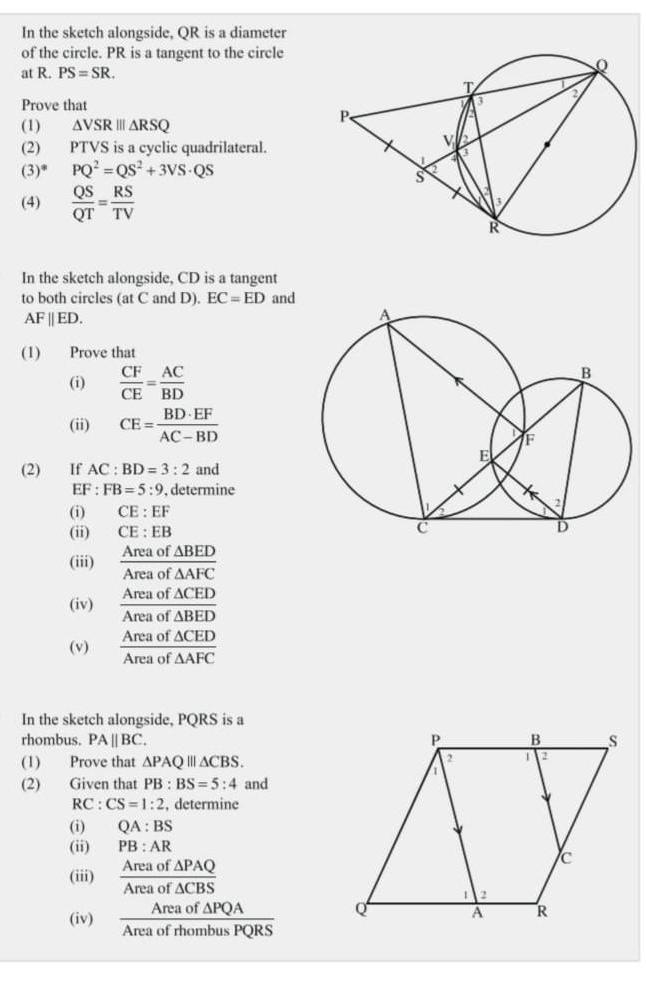
In the sketch alongside, QR is a diameter of the circle. PR is a tangent to the circle at R. PS= SR. Prove that (1) (2) (3)* In the sketch alongside, CD is a tangent to both circles (at C and D). EC=ED and AF || ED. (1) (2) AVSR ||| ARSQ PTVS is a cyclic quadrilateral. PQ =QS +3VS-QS QS RS = QT TV (1) (2) Prove that CF (i) CE CE= (ii) If AC: BD= 3:2 and EF: FB 5:9, determine (i) (ii) (iii) (iv) AC BD BD EF AC-BD CE: EF CE : EB Area of ABED Area of AAFC Area of ACED In the sketch alongside, PQRS is a rhombus. PA || BC. (iv) Area of ABED Area of ACED Area of AAFC Prove that APAQ ||| ACBS. Given that PB: BS=5:4 and RC: CS 1:2, determine (i) QA: BS (ii) PB: AR Area of APAQ (iii) Area of ACBS Area of APQA Area of rhombus PQRS